Binomialverteilung
Inhaltsverzeichnis
\(\\\)
Definition der Binomialverteilung
Die Binomialverteilung hat nur zwei mögliche Merkmalsausprägungen, Treffer und Niete. Außerdem ist die Wahrscheinlichkeit für das Ereignis stets gleich. Das entspricht einem Zufallsversuch mit Zurücklegen.
\(\\[2em]\)
Wahrscheinlichkeitsbaum der Binomialverteilung
Zur Veranschaulichung wird ein Wahrscheinlichkeitsbaum für einen Würfelversuch bei viermaligen Werfen des Würfels. Das Ereignis sei dreimal eine \(2\) zu würfeln.
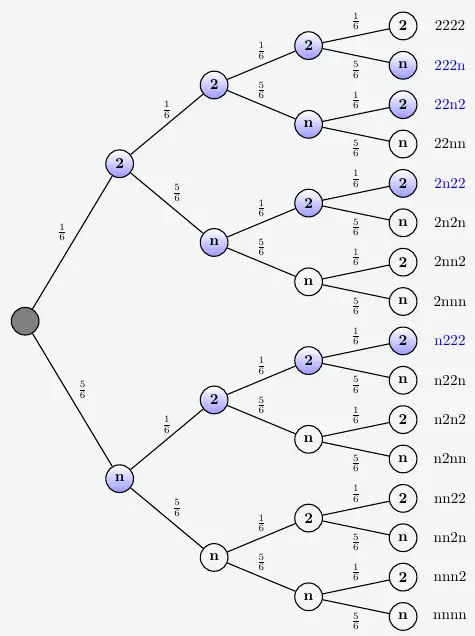
\(\\[2em]\)
Bernoullikette
Es gilt das Ereignis
\( E \, = \, \{ 222n \, , \; 22n2 \, , \; 2n22 \, , \; n222 \} \)
\(\\\)
Mit den Pfadregel erhalten wir die Wahrscheinlichkeit
\( \begin{array}{ r c l } P(E) & = & P(222n) + P(22n2) + P(2n22) + P(n222) \\[6pt] P(E) & = & \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{5}{6} + \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{5}{6} \cdot \frac{1}{6} +\frac{1}{6} \cdot \frac{5}{6} \cdot \frac{1}{6} \cdot \frac{1}{6} + \frac{5}{6} \cdot \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{1}{6} \\[6pt] P(E) & = & 4 \cdot \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{5}{6} \\[6pt] P(E) & = & 4 \cdot \left(\frac{1}{6}\right)^3 \cdot \left(\frac{5}{6}\right)^1 \\[6pt] \end{array} \)
\(\\\)
Übertragen auf beliebige Wahrscheinlichkeitsbäume einer Binomialverteilung entsteht damit die Formel von Bernoulli :
\( P( x = k) \; = \, \begin{smallmatrix} \renewcommand{\arraystretch}{0.9} \left( \begin{array}{c} n \\ k \end{array} \right) \renewcommand{\arraystretch}{1} \end{smallmatrix} p^k \cdot (1-p)^{n-k} \)
\(\\\)
Dabei
-
berechnet \(\begin{smallmatrix} \renewcommand{\arraystretch}{0.9} \left( \begin{array}{c} n \\ k \end{array} \right) \renewcommand{\arraystretch}{1} \end{smallmatrix} \) die Anzahl der möglichen Pfade (Kombinationen),
-
gibt \(n\) bezogen auf einen Würfelversuch die Anzahl der Würfe,
-
gibt \(x\) bzw. \(k\) die Anzahl der Treffer und
-
\(p\) die Wahrscheinlichkeit eines Treffers
an.
\(\\[2em]\)
Wahrscheinlichkeitsverteilung
Wir betrachten nun eine Verteilung mit einer Bernoullikette von der Länge \(n=10\) und der Wahrscheinlichkeit \(p=0{,}6\). Für die Wahrscheinlichkeitsverteilung werden alle möglichen \(k\) notiert, hier also mit den \(k\)-Werten von \(0\) bis \(10\).
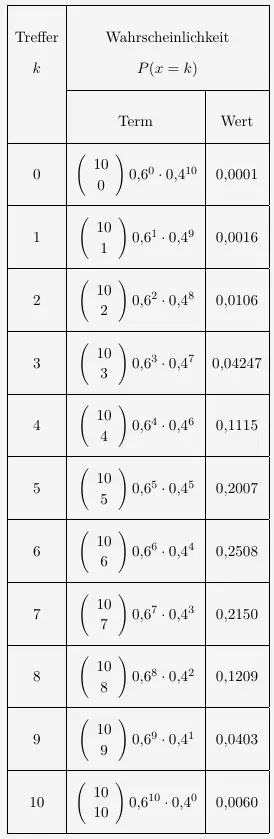
\(\\[2em]\)
Diskrete Verteilung
Verteilungen sind eingeteilt in diskrete (abzählbare) und stetige Verteilungen.

\(\\\)
Binomialverteilungen sind diskret. Unsere Verteilung stellt sich graphisch wie folgt dar.
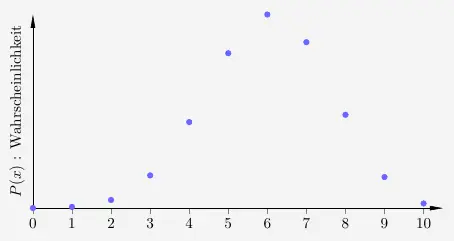
Wie hier zu sehen ist kommen nur die ganzzahligen \(x\)-Werte im Bereich von \(0\) bis \(10\) vor.
Die entsprechende stetige Funktion, wie oben abgebildet, ist die Normalverteilung.
\(\\[2em]\)
Histogramm der Wahrscheinlichkeitsverteilung
In der Regel wird die Binomialverteilung jedoch nicht als Punktdiagramm, sondern als Histogramm dargestellt. Das hat den Vorteil, das jede einzelne Wahrscheinlichkeit durch die Flächegröße eines Streifens dargestellt werden kann. Alle Streifen zusammen bilden die Wahrscheinlichkeitsverteilung ab.
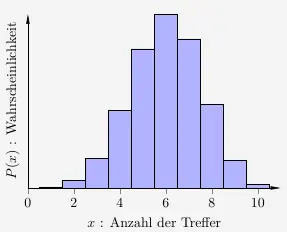
Im Histogramm ist die Streifenbreite exakt \(1\) ist. Der \(k\)–te Streifen reicht also von \(k - 0{,}5\) bis \(k + 0{,}5\).
Alle Streifen zusammen sind \(100\%\) und haben die Wahrscheinlichkeit \(1\).
\(\\[2em]\)
Kumulierte Wahrscheinlichkeit
Unter kumulierter (gehäufter) Wahrscheinlichkeit versteht man die aufsummierten Wahrscheinlichkeiten bis zu einer Stelle \(k\) und wird geschrieben als \(P( x \leq k)\). Zum Beispiel ist
\( P( x \leq 4) \, = \, P( x = 0) + P( x = 1) + P( x = 2) + P( x = 3) + P( x = 4) \)
\(\\\)
oder
\( P( x \leq 5) \, = \, P( x = 0) + P( x = 1) + P( x = 2) + P( x = 3) + P( x = 4) + P( x = 5) \)
\(\\\)
Demnach können wir auch schreiben
\( P( x \leq 5) \, = \, P( x \leq 4) + P( x = 5) \)
\(\\\)
Daraus folgt
\( P( x = 5) \, = \, P( x \leq 5) - P( x \leq 4) \)
\(\\\)
Entsprechend können auch Bereiche formuliert werden.
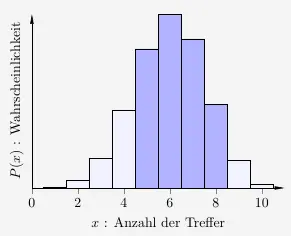
\( P( 5 \leq x \leq 8) \, = \, P( x \leq 8) - P( x \leq 4) \)
\(\\\)
Auch Bereiche rechts von \(k\) lassen sich ausdrücken.
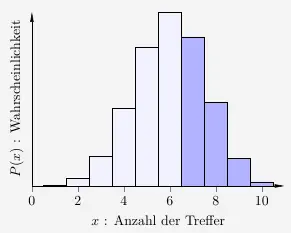
\( P( x > 6) \, = \, P( x \leq 10) - P( x \leq 6) \, = \, 1 - P( x \leq 6) \)
\(\\\)
\(P( x \leq 10)\) sind natürlich \(100\%\), also \(1\).
\(\\\)
Um die kumulierte Wahrscheinlichkeit zu bestimmen ist es in der Regel unpraktikabel alle einzelnen Wahrscheinlichkeiten auszurechnen. Der herkömmliche Taschenrechner bietet dazu Taschenrechnerfunktionen für Verteilungen an.
Ist der Taschenrechner nicht mit einer solcher Funktion ausgestattet, so gibt es noch den Weg, die kumulierten Werte aus entsprechenden Tabellen abzulesen.
\(\\[1em]\)