Vierfeldertafel
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – vollständige Vierfeldertafel
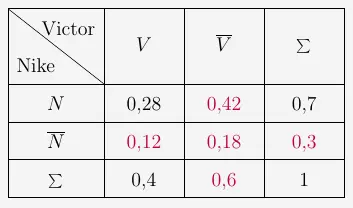
\(\\[2em]\)
Aufgabe 2 – ein Pfeil landet im Zentrum
Hier handelt es sich um eine bedingte Wahrscheinlichkeit, denn die Voraussetzung ist, dass Nike trifft oder Victor trifft. In der Mengenschreibweise wäre das
\( \quad \left(N \cap \overline{V}\right) \cup \left(\overline{N} \cap V\right) \)
\(\\\)
Wir berechnen die bedingte Wahrscheinlichkeit mit
\(\\\) \( \quad \begin{array}{ r c l } P_{\text{einer trifft}}( \text{Nike trifft} ) & = & \frac{P(\text{einer trifft}) \; \cap \; P(\text{Nike trifft}) }{P(\text{einer trifft})} \\ \end{array} \)
\(\\\)
Da “Nike trifft” eine Teilmenge von “einer trifft” ist gilt
\(\\\)
\( \quad \begin{array}{ r c l } P_{\text{einer trifft}}( \text{Nike trifft} ) & = & \frac{P(\text{Nike trifft}) }{P(\text{einer trifft})} \\[8pt] & = & \frac{P(N \; \cap \; \overline{V}) } {P\left((N \; \cap \; \overline{V}) \; \cup \; (\overline{N} \; \cap \; V)\right)} \\[8pt] & = & \frac{P(N \; \cap \; \overline{V}) }{P(N \; \cap \; \overline{V}) \; + \; P(\overline{N} \; \cap \; V)} \\[8pt] & = & \frac{0{,}42 }{0{,}42 \; + \; 0{,}12} \\[8pt] & = & 0{,}7 \\[6pt] & = & 70\% \\ \end{array} \)
\(\\[2em]\)
Aufgabe 3 – Treffer gewinnt
Der Wahrscheinlichkeitsbaum des Spiels stellt sich folgendermaßen dar.

\(\\\)
Die Ereignismenge dafür, dass Victor gewinnt ist
\( \quad E_V \; = \; \left\{ (V) \; , \; (\overline{V} , \overline{N} , V) \; , \; (\overline{V} , \overline{N} , \overline{V} , \overline{N} , V) \; , \; (\overline{V} , \overline{N} , \overline{V} , \overline{N} , \overline{V} , \overline{N}) \right\} \)
\(\\\)
Daraus ergibt sich die Wahrscheinlichkeit
\( \quad \begin{array}{ r c l } P \left( E_V \right) & = & 0{,}4 \\[5pt] & & + \; 0{,}6 \cdot 0{,}3 \cdot 0{,}4 \\[5pt] & & + \; 0{,}6 \cdot 0{,}3 \cdot 0{,}6 \cdot 0{,}3 \cdot 0{,}4 \\[5pt] & & + \; 0{,}6 \cdot 0{,}3 \cdot 0{,}6 \cdot 0{,}3 \cdot 0{,}6 \cdot 0{,}3 \\[8pt] & = & 0{,}490792 \\[6pt] & = & 49{,}0792\% \\ \end{array} \)
\(\\\)
Die restlichen Prozente müssten auf Nike entfallen. Zur Kontrolle, was aber nicht notwendig wäre, berechnen wir die Wahrscheinlichkeit für Nike. Zunächst die Ereignismenge:
\( \quad E_N \; = \; \left\{(\overline{V} , N) \; , \; (\overline{V} , \overline{N} , \overline{V} , N) \; , \; (\overline{V} , \overline{N} , \overline{V} , \overline{N} , \overline{V} , N) \right\} \)
\(\\\)
Daraus ergibt sich die Wahrscheinlichkeit
\( \quad \begin{array}{ r c l } P\left( E_V \right) & = & 0{,}6 \cdot 0{,}7 \\[5pt] & & + \; 0{,}6 \cdot 0{,}3 \cdot 0{,}6 \cdot 0{,}7 \\[5pt] & & + \; 0{,}6 \cdot 0{,}3 \cdot 0{,}6 \cdot 0{,}3 \cdot 0{,}6 \cdot 0{,}7 \\[8pt] & = & 0{,}509208 \\[6pt] & = & 50{,}9208\% \\ \end{array} \)
\(\\\)
Damit hat Nike die besseren Gewinnchancen.
\(\\\)