HMF 3
Analysis (Pool 2)
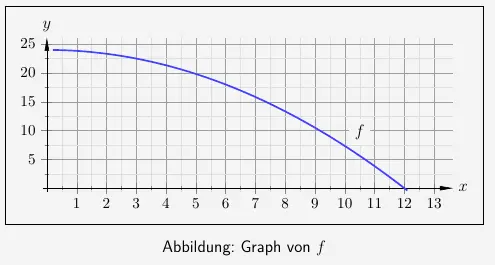
Im Koordinatensystem ist der Graph der Funktion \(f\) mit
\( \quad f(x) = 24 - \frac{1}{6}x^2 \)
dargestellt.
Für jede Zahl \(x\) mit \(0<x<12\) wird ein Rechteck \(R_x\) durch die Punkte \((0|0)\), \((x|0)\), \(\big(x|f(x)\big)\) und \(\big(0|f(x)\big)\) festgelegt.
\(\qquad \qquad \qquad\)
\(\\\)
Aufgabe 1
Zeichnen Sie das Rechteck \(R_6\) in das Koordinatensystem.
(1 P)
\(\\\)
Aufgabe 2
Unter allen Rechtecken \(R_x\) gibt es eines mit maximalem Flächeninhalt
\( \quad A(x) = x \cdot f(x) \)
Untersuchen Sie, ob für dieses Rechteck \(x<7\) ist.
(4 P)
\(\\[2em]\)