Hypothesentest

---

\(\\\)

Aufgabe 1 – Signifikanztest

\(x\) beschreibt die Anzahl der der Schüsse mit dem neuen Bogen, die ins Zentrum treffen und ist binomialverteilt mit \(n=150\).

Im Grunde arbeiten wir wie bei einem Alternativtest mit 2 Hypothesen, die wir gegeneinander abwägen. Die Vermutung von Nike stellt dabei die Hypothese \(h_1\) dar. Da beim Signifikanztest dies die einzige Hypothese ist, konstruieren wir eine Gegenhypothese, die Hypothese \(h_0\).

\( \begin{array}{ r l l } h_1 : & p_1 > 0{,}7 & \textit{als zu beweisende Hypothese} \\[6pt] h_0 : & p_0 \leq 0{,}7 & \textit{als Nullhypothese} \\ \end{array} \)

\(\\\)

Laut Aufgabenstellung sollen wir eine Entscheidungsregel dafür aufstellen, wann die Vermutung von Nike als richtig gilt. Das erreichen wir dadurch, indem wir feststellen, wann die Gegenhypothese nicht eintreten kann.

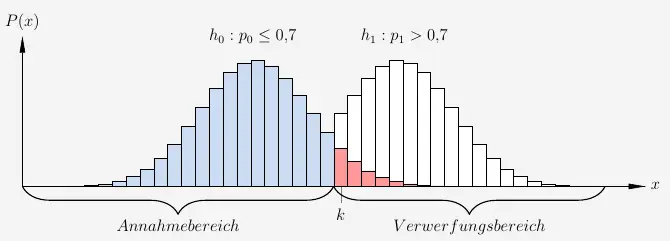
Der Verwerfungsbereich enthält nun die Anzahl an Treffern, bei denen wir die Hypothese \(h_0\) ablehnen und damit die Hypothese \(h_1\) annehmen würden. Entsprechend gibt der Annahmebereich die Anzahl an Treffern an, bei denen wir die Hypothese \(h_0\) befürworten würden.

Es gilt

\( \quad \begin{array}{ r c l } V & = & [k ; 150] \\[6pt] A & = & [0 ; k-1] \\ \end{array} \)

\(\\\)

Der kritische Wert \(k\) bezeichnet die Grenze, die auch \(g\) genannt wird, zwischen dem Annahmebereich und dem Verwerfungsbereich (Ablehnungsbereich). Dabei wird \(k\) dem Verwerfungsbereich zuordnet. In diesem Fall ist \(k\) die Grenze \(g_r\), denn die Grenze liegt auf der rechten Seite von \(h_0\). Es handelt sich hier um einen rechtsseitigen Signifikanztest, denn \(h_0\) wird nach rechts gegen \(h_1\) abgegrenzt.

Das Signifikanzniveau von \(5\%\) gibt die Größe des Verwerfungsbereiches an und ist zugleich ein Synonym für den Fehler 1. Art.

Wir berechnen \(k\) ausgehend von \(n=150\) und \(p=0{,}7\) mit der Gleichung

\( \quad P(x \geq k) \leq 0{,}1 \)

\(\\\)

Von links gelesen ist das

\( \quad P(x \leq k) \geq 0{,}9 \)

\(\\\)

Das \(k\) kann nun auf verschiedene Weise bestimmt werden. Ich nenne hier nun 4 übliche Möglichkeiten:

• Bestimmung von \(k\) mithilfe der Tabellen für kumulierte Binomialverteilungen
• Bestimmung von \(k\) über Probieren
• Bestimmung von \(k\) mithilfe der \(\sigma\)-Umgebung
• Bestimmung von \(k\) mithilfe der Taschenrechnerfunktion für die Normalverteilung

\(\\[2em]\)

k bestimmen mit kumulierten Binomialverteilungen

k mit Tabellen ermitteln

Wir wählen die Tabelle für kumulierte Binomialverteilungen mit \(n=150\).

Da wir mit der Trefferwahrscheinlichkeit \(p=0{,}7> 0{,}5\) arbeiten, müssen wir von unten und von rechts ablesen. Das bedeutet, dass wir

\( \quad P(x \leq k)=0{,}9 \)

\(\\\)

umrechnen müssen in der Art

\( \quad P(y \leq k) \; = \; 1 - 0{,}9 \; = \; 0{,}1 \)

\(\\\)

Da wir einen Wert benötigen für \(P(x \leq k)>0{,}9\) suchen wir entsprechend den Wert für \(P(y \leq k)<0{,}1\).

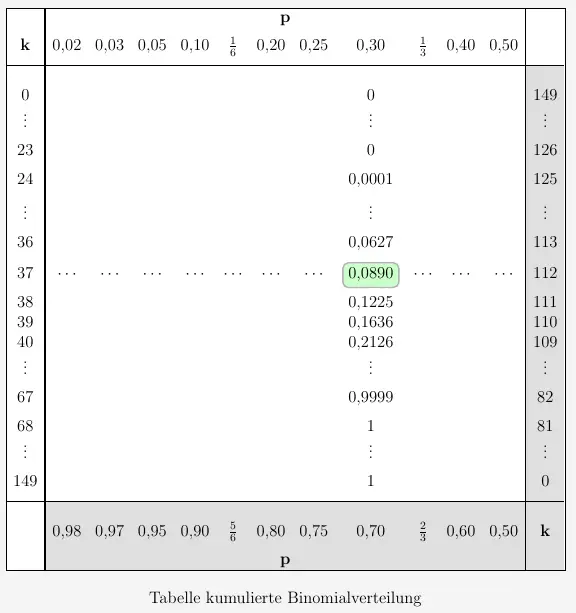
Wir erhalten den Annahme- und Verwerfungsbereich mit

\( \quad V=[112 , 150] \quad \text{und} \quad A=[0 ; 111] \)

\(\\\)

Entscheidungsregel:

Landet Nike bei \(150\) Schüssen \(112\) oder mehr Treffer, so können wir davon ausgehen, dass sie mit dem neuen Bogen ihre Trefferquote verbessern kann.

\(\\[2em]\)

Probieren mit dem Taschenrechner

Wie wir hier sehen können,

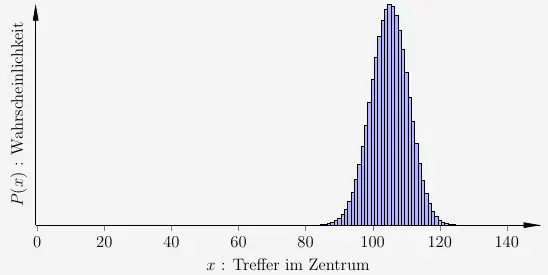
kommen die meisten \(x\)-Werte für \(k\) nicht infrage. Eine gute Methode ist, das \(k\) rechts vom Erwartungswert, also der Wert mit der größten Wahrscheinlichkeit, zu suchen.

Der Erwartungswert ist

\( \quad \mu \; = \; n \cdot p \; = \; 150 \cdot 0{,}7 \; = \; 105 \)

\(\\\)

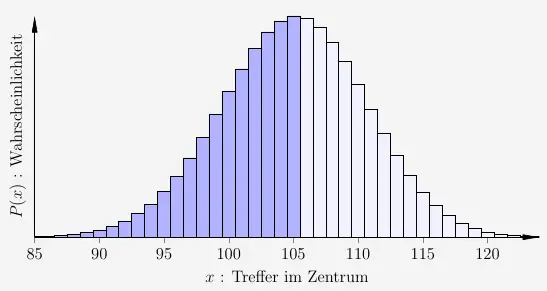
Bis zum Erwartungswert haben wir nahezu \(50\%\) der Fläche. Von dort an fallen die Wahrscheinlichkeiten meist schnell ab.

Um festzustellen, wann \(90\%\) überschritten wird, wählen wir zunächst die ersten \(10\) \(x\)-Werte rechts von \(\mu\).

Mit dem Casio fx-DE X gehen wir mit \(\boxed{Menu}\) \(\boxed{7}\) ▼ zu den kumulierten Binomialverteilungen.

Wir wählen \(\boxed{1}\)

\(\\\)

und noch einmal \(\boxed{1}\). Wir tragen für \(k\) die Zahlen von \(206\) bis \(115\) ein. Jede Eingabe wird mit \(\boxed{=}\) bestätigt.

\(\\\)

Nach der letzten Eingabe betätigen wir zweimal \(\boxed{=}\).

\(\\\)

Nach der letzten Eingabe betätigen wir wieder zweimal \(\boxed{=}\).

\(\\\)

Mit den Pfeiltasten bewegen wir uns nach unten.

\(\\\)

Wir sehen, dass bei \(112\) Treffern die \(90\%\) erstmals überschritten wird.

Wir erhalten den Annahme- und Verwerfungsbereich mit

\( \quad V=[112 , 150] \quad \text{und} \quad A=[0 ; 111] \)

\(\\\)

Entscheidungsregel:

Landet Nike bei \(150\) Schüssen \(112\) oder mehr Treffer, so können wir davon ausgehen, dass sie mit dem neuen Bogen ihre Trefferquote verbessern kann.

\(\\[2em]\)

k bestimmen mit der Normalverteilung

Rechnerisch kann die Stelle \(g\), also die Grenze zwischen den blauen und den grauen Streifen, durch die Berechnung der Fläche mithilfe des Integrals einer Funktion ermittelt werden.

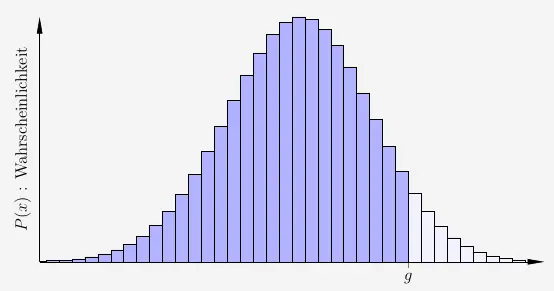
Das Problem dabei ist, das es sich bei der Binomialververteilung aber nicht um eine stetige Funktion, sondern um eine diskrete Funktion handelt. Das bedeutet, dass nur ganzzahlige \(x\)-Werte vorkommen und wir es mit einer Punktmenge zu tun haben.

Die Integralrechnung lässt sich hier nicht anwenden. Was machen wir jetzt?

Die Lösung ist, die Binomialverteilung in eine stetige Funktion zu transformieren.
Und dabei bietet sich die Normalverteilung an, die näherungsweise dem Verlauf der Binomialverteilung wiedergibt.

Bitte weiterlesen bei der Sigma-Umgebung oder der Taschenrechnerfunktion für die Normalverteilung.

\(\\[2em]\)

Sigma-Umgebung

Bei der Normalverteilung ist jede Flächengröße einem Radius \(z\) zugeordnet, so dass wir uns nicht um das Integral der Funktion \(\varphi(z)\) kümmern müssen. Betrachten wir jetzt den Radius.

Der Radius ist ein Maß für die \(\sigma\)-Umgebung der Binomialverteilung und steht im direkten Zusammenhang zur Flächengröße.

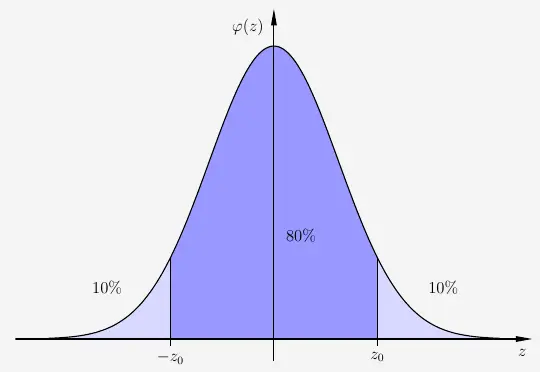
In der Normalverteilung, bei der \(\sigma=1\) ist, ist \(z\), hier bei \(z_0\), der Wert auf der \(z\)-Achse. Da der Radius in der \(\sigma\)-Umgebung die Abweichung vom Erwartungswert sowohl nach links als auch nach rechts angibt, müssen wir mit einer \(\sigma\)-Umgebung von 80% ausgehen.

In den Tabellenwerken befinden sich alle Radien bis \(z=3\) auf zwei Kommastellen genau mit der zugehörigen \(\sigma\)-Umgebung.

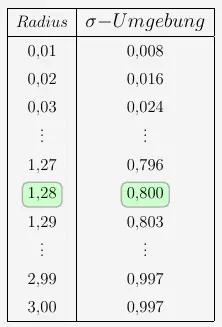
Bei der 80%igen \(\sigma\)-Umgebung erhalten wir \(z_0=1{,}28\). Mit der Umrechnung

\( \quad g_r = \mu + z_0 \cdot \sigma \)

\(\\\)

können wir das \(k\) der Binomialverteilung ermitteln. Wir rechnen mit

\( \quad \mu = n \cdot p = 150 \cdot 0{,}7 = 105 \)

\(\\\)

und

\( \quad \sigma = \sqrt{n \cdot p \cdot (1-p)} = \sqrt{150 \cdot 0{,}7 \cdot (1-0{,}7)} = 5{,}61 > 3 \)

\(\\\)

Die LaPlace-Bedingung \(\sigma > 3\) gewährleistet, dass wir die Normalverteilung als gute Näherung der Binomialverteilung verwenden dürfen.

\( \quad g_r = 105 + 1{,}28 \cdot 5{,}61 = 112{,}1808 \)

\(\\\)

\(g_r\) liegt am Ende des letzten Streifens. Den richtigen Wert erhalten wir mit

\( \quad g_r - 0{,}5 = 112{,}1808 - 0{,}5 = 111{,}6808 \)

\(\\\)

Wir erhalten den Annahme- und Verwerfungsbereich mit

\( \quad A=[0 ; 111] \quad \text{und} \quad V=[112 , 150] \)

\(\\\)

Entscheidungsregel:

Landet Nike bei \(150\) Schüssen \(112\) oder mehr Treffer, so können wir davon ausgehen, dass sie mit dem neuen Bogen ihre Trefferquote verbessern kann.

\(\\[2em]\)

Taschenrechnerfunktion für die Normalverteilung

Der Taschenrechner bedient sich der Integralrechnung mit

Dabei soll nun gelten, dass die Stammfunktion

\( \quad \Phi (z_0) = 0{,}9 \)

\(\\\)

ist. Um \(z_0\) direkt in das \(k\) der Binomialverteilung

umzurechnen wird mit

\( \quad \Phi \left( \frac{k + 0{,}5 - \mu}{\sigma} \right) \)

\(\\\)

gearbeitet. Dabei ist

\( \quad \mu = n \cdot p = 150 \cdot 0{,}7 = 105 \)

\(\\\)

und

\( \quad \sigma = \sqrt{n \cdot p \cdot (1-p)} = \sqrt{150 \cdot 0{,}7 \cdot (1-0{,}7)} = 5{,}61 \)

\(\\\)

Mit der Umkehrfunktion (inverse Funktion)

\( \quad k + \, 0{,}5 = \Phi_{\mu ; \sigma}^{-1}(0{,}9) = \Phi_{105 ; 5{,}61}^{-1}(0{,}9) \)

\(\\\)

berechnen wir das \(k\). Bei dem Casio fx-DE X geben wir \(\boxed{Menu}\) \(\boxed{7}\) ein.

Wir wählen die inverse Normalverteilung mit \(\boxed{3}\) und geben folgende Werte ein.

\(\\\)

Dabei bestätigen wir jede Eingabe mit \(\boxed{=}\) und drücken anschließend noch einmal \(\boxed{=}\).

\(\\\)

\(\\\)

Wir erhalten

\( \quad \begin{array}{ r c l l } k + 0{,}5 & = & 112{,}1895047 & | - 0{,}5 \\[6pt] k & = & 111{,}6895047 \\ \end{array} \)

\(\\\)

Damit lautet der Annahme- und Verwerfungsbereich

\( \quad A=[0 ; 111] \quad \text{und} \quad V=[112 , 150] \)

\(\\\)

Entscheidungsregel:

Landet Nike bei \(150\) Schüssen \(112\) oder mehr Treffer, so können wir davon ausgehen, dass sie mit dem neuen Bogen ihre Trefferquote verbessern kann.

\(\\[2em]\)

Aufgabe 2 – Fehler 2. Art

Der Fehler 2. Art besagt, dass eine falsche Hypothese nicht verworfen wird.

Im Sachzusammenhang bedeutet dies folgendes:
Durch den neuen Bogen verbessert sich die Trefferquote von Nike tatsächlich. Es ist \(p>0{,}7\) also richtig.

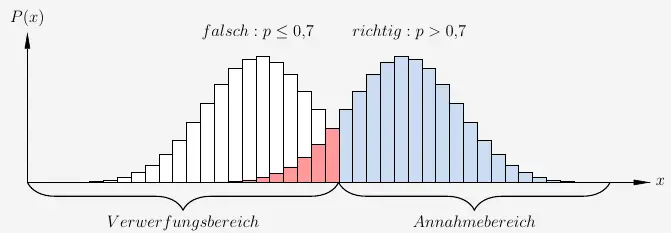
Angenommen Nike erzielt mit dem neuen Bogen bei den 150 Schüssen nur 110 Treffer. Sie würde die Entscheidung fällen, dass sie mit dem neuen Bogen auch nur eine Trefferquote von 70% oder eventuell sogar noch weniger hat.

Dieses Risiko eine falsche Entscheidung zu fällen beschreibt der Fehler 2. Art.

Der Fehler 2. Art, der \(\beta\)-Fehler, ist also das Risiko sich für die Hypothese \(p \leq 0{,}7\) aufgrund der Stichprobenergebnisses zu entscheiden, obwohl dieses die falsche Hypothese ist.

Für die Berechnung bleiben die Grenzen die gleichen wie zuvor. Nur sind jetzt der Annahme und Verwerfungsbereich vertauscht.

\( \quad V=[0 ; 111] \quad \text{und} \quad A=[112 , 150] \)

\(\\\)

Wir rechnen dieses Mal mit \(p = 0{,}75\) die kumulierte Wahrscheinlichkeit aus.

\( \quad \beta \; =\; P_{150 ; 0{,}75}(x \leq 111) \; =\; 0{,}4193 \; =\; 41{,}93 \% \)

\(\\\)