Aufgaben

---

\(\\\)

“Notre-Dame”

Im Jahr \(2019\) zerstörte ein Großbrand das Dach der Kathedrale Notre-Dame de Paris. Eine der vielen Ideen für den geplanten Wiederaufbau sieht die Errichtung eines Glasdaches mit einem gläsernen Turm darauf vor.

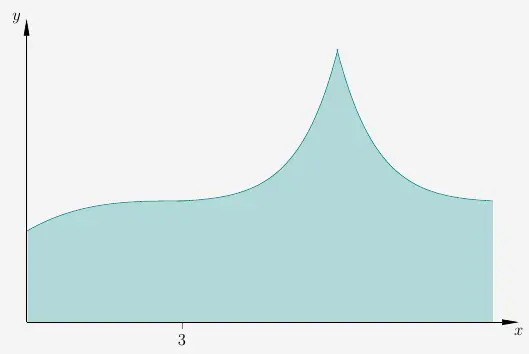
In einem geeigneten Koordinatensystem wird der Dachfirst mit Hilfe von Funktionsgraphen modelliert. Die Funktionswerte geben die Höhe des Dachfirsts über dem Boden an; Die \(x\)-Achse beschreibt das Bodenniveau. Dabei entspricht eine Längeneinheit \(10 \, m\) in der Wirklichkeit.

\(\\[1em]\)

Funktion f

Zunächst wird eine ganzrationale Funktion \(f\) dritten Grades betrachtet. Der Graph von \(f\) verläuft durch die beiden Punkte \(P(0|3)\) und \(W(3|4)\). Dabei ist \(W\) ein Wendepunkt mit waagerechter Tangente. Mit Hilfe des Graphen von \(f\) wird über dem Intervall \([0;3]\) ein erstes Teilstück des Dachfirsts modelliert.

\(\\[1em]\)

1. Leiten Sie einen Funktionsterm von \(f\) her.

\(\qquad \big[\text{Zur Kontrolle: } \; f(x) \; = \; \frac{1}{27} x^3 - \frac{1}{3} x^2 + x + 3 \big]\)

(6 P)

\(\\\)

2. Berechnen Sie die Höhe des Dachfirsts über dem Boden an der Stelle \(x = 1\).

   (2 P)

\(\\\)

3. Geben Sie einen Funktionsterm der Ableitungsfunktion \(f'\) und die Steigung des Graphen von \(f\) an der Stelle \(x = 0\) an.

   (2 P)

\(\\\)

4. Weisen Sie mit Hilfe einer Rechnung nach, dass der Graph von \(f\) für \(x < 3\) rechtsgekrümmt ist.

   (3 P)

Lösung

\(\\[2em]\)

Funktion g

Nun werden eine Funktion \(g\) und ihre Ableitungsfunktion \(g'\) mit

\( \quad g(x) \; = \; (x - 3) e^{x - 5{,}5} + 4 \quad \text{und} \quad g'(x) \; = \; (x - 2) e^{x - 5{,}5} \)

betrachtet. Mit Hilfe des Graphen von \(g\) wird über dem Intervall \([3;6]\) ein weiteres Teilstück des Dachfirsts modelliert.

\(\\[1em]\)

1. Ergänzen Sie die Wertetabelle zu \(g\) auf dem Arbeitsblatt

\(\qquad \qquad \qquad \quad\) Abbildung ausdrucken

\(\\\)

und zeichnen Sie den Graphen von \(g\) über dem Intervall \([3;6]\) in das dort vorgegebene Koordinatensystem.

(4 P)

\(\\\)

2. Die Graphen von \(f\) und \(g\) verlaufen beide durch den Punkt \(W(3|4)\).
   Prüfen Sie, ob der Dachfirst dort knickfrei modelliert wird.

   (3 P)

\(\\\)

3. Bestimmen Sie alle Extrem- und Wendestellen der auf ganz \(\mathbb{R}\) definierten Funktion \(g\).

   (8P)

\(\\\)

4. Der Graph der Funktion \(g\) wird an der \(y\)-Achse gespiegelt und dann um zwölf Längeneinheiten nach rechts verschoben. Dadurch ergibt sich der Graph der Funktion \(g^*\), der über dem Intervall \([6;9]\) auf dem Arbeitsblatt gezeigt wird.
   Ermitteln Sie einen Funktionsterm \(g^*(x)\), und stellen Sie diesen Term in der Form

\(\qquad (ax + b) \cdot e^{- x + c} + 4\)

mit geeigneten reellen Werten \(a\), \(b\) und \(c\) dar.

(4 P)

Lösung

\(\\[2em]\)

Funktionenschar h_k

Für eine verbesserte Modellierung des Dachfirsts wird anstelle der Funktion \(g\) die Verwendung der Funktionen \(h_k\) und ihrer Ableitungsfunktionen \(h_k'\) mit

\(\quad h_k(x) \; = \; \dfrac{5}{9}(x - 3)^2 e^{k(x - 6)} + 4\)

\(\\\) und

\(\quad h_k'(x) \; = \; \frac{5}{9}(x - 3)(kx -3k +2) e^{k(x - 6)}\)

\(\\\)

mit \(k \geq 0\) vorgeschlagen.

\(\\[2em]\)

1. Weisen Sie nach, dass die Funktion \(g\) nicht in der Schar der Funktionen \(h_k\) enthalten ist.

   (2 P)

\(\\\)

2. Zeigen Sie, dass der Term \(5k + \frac{10}{3}\) die Steigung des Graphen von \(h_k\) an der Stelle \(x = 6\) angibt.

   (2 P)

\(\\\)

3. So wie in der Teilaufgabe 4) der Aufgabe der \(\textit{Funktion g}\) lässt sich aus dem Graphen von \(h_k\) der Graph einer Funktion \(h_k^*\) erzeugen. Bei \(x = 6\) modellieren die Graphen von \(h_k\) und \(h_k^*\) dann die Spitze des Dachfirsts.
   Bestimmen Sie denjenigen Wert für \(k\), für den der Innenwinkel der Spitze \(30^{\circ}\) beträgt.

   (4 P)

Lösung

\(\\[2em]\)