Maßzahlen der Gehwegplatte
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Funktionsterm von r
Der Graph von \(r\) ergibt sich indem \(l\) 6 Einheiten nach rechts verschoben wird. Das erreichen wir durch eine Verringerung des \(x\) um 6. Es ergibt sich
\(\quad \begin{array}{ r c l } r(x) & = & 2 \cdot \big( ( x - 6) + 1 \big) \cdot e^{-0{,}73 \cdot (x - 6)} \\[6pt] & = & 2 \cdot ( x - 5) \cdot e^{-0{,}73 \cdot (x - 6)} \\ \end{array} \)
\(\\\)
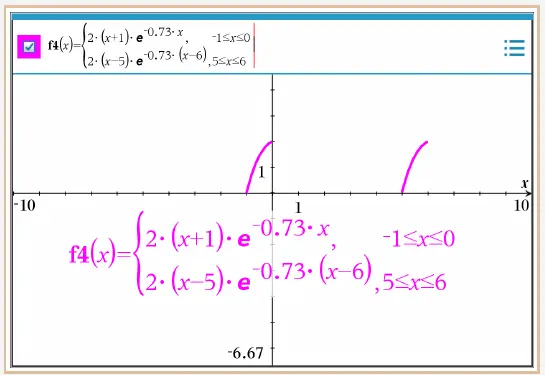
Um die Richtigkeit der Funktion zu zeigen, können wir den Graphen von \(r\) im Graphik-Modus zeichnen lassen. Hier bietet es sich nun an, die beiden Funktionen \(l\) und \(r\) als abschnittsweise Funktion \(g\) darzustellen mit
\(\quad g(x) \; = \; \left\{ \begin{array}{ r c r } l(x) & {,} & -1 \leq x \leq 0 \\[6pt] r(x) & {,} & 5 \leq x \leq 6 \\ \end{array} \right. \)
\(\\\)
Für abschnittsweise Funktionen verwenden wir folgendes Werkzeug

\(\\\)
und setzen es im Graphik-Modus ein.
\(\\[2em]\)
Aufgabe 2 – Flächeninhalt der Form
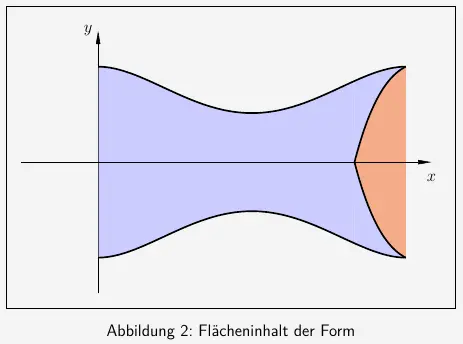
Der Flächeninhalt der Form

\(\\\)
entspricht dieser dargestellten Fläche,
\(\\\)
denn die doppelte Fläche unter der Funktion \(l\) im Intervall \([-1 ; 0]\) (rotbraune Fläche links) muss genauso groß sein wie die doppelte Fläche unter der Funktion \(r\) im Intervall \([5 ; 6]\) (rotbraune Fläche rechts). Denn \(r\) ist ja die um \(6 \, dm\) verschobene Funktion \(l\).
Die blaue und rotbraune Fläche zusammen genommen sind also genau die doppelte Fläche unter der Funktion \(f\) im Intervall \([0 ; 6]\).

\(\\\)
Demnach beschreibt der Term
\(\quad 2 \cdot \displaystyle{\int}_0^6 f(x) \, dx \)
exakt den Flächeninhalt der Form.
\(\\[2em]\)
Aufgabe 3 – Masse der Form
Um die Masse der Form in Kilogramm zu bestimmen muss das Volumen mit \(1{,}76\) multipliziert werden. Das Volumen berechnet sich mit
\(\quad V \; = \; \textit{Grundfläche} \cdot \textit{Höhe} \)
\(\\\)
Die Masse berechnet sich nun wie folgt:

\(\\\)
Die Gehwegplatte wiegt ungefähr \(15{,}65 \, kg\).
\(\\[2em]\)
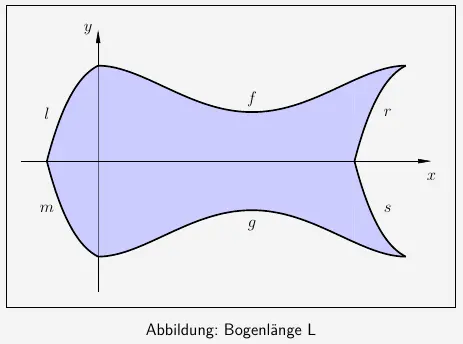
Aufgabe 4 – Bogenlänge L
Die Graphen \(l\) , \(m\) , \(r\) und \(s\) haben jeweils die gleiche Länge.
\(\\\)
Ebenso sind die Graphen \(f\) und \(g\) gleich lang. Daraus ergibt sich der Umfang \(U\) der Form mit
\(\quad U \; = \; 4 \cdot \displaystyle{\int}_{-1}^0 \sqrt{1 + \big( l'(x) \big)^2} \, dx +2 \cdot \displaystyle{\int}_0^6 \sqrt{1 + \big( f'(x) \big)^2} \, dx \)
\(\\\)
Wir definieren Funktion \(l\) und deren Ableitung

\(\\\)
und berechnen den Umfang.
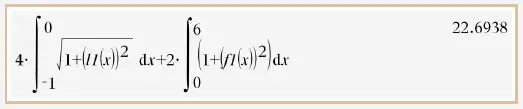
\(\\\)
Der Umfang der Form beträgt also \(22{,}6938 \, dm \approx 2{,}27 \, m\) .
Zum Vergleich erhalten wir mit einem anderen Taschenrechner \(2{,}19 \, m\). Uns soll aber das berechnete Ergebnis genügen.
\(\\\)