Ganzrationale Funktionen
Inhaltsverzeichnis
\(\\\)
Ganzrationale Funktionen, auch Polynomfunktionen oder Polynome genannt, sind eine Summe von Potenzfunktionen. Beispielsweise besteht die Polynomfunktion
\( \quad f(x) = \frac{1}{2}x^3 -2x^2 + \frac{2}{3}x + 1 \)
\(\\\)
aus den Potenzfunktionen
\( \quad \begin{array}{ l } \bullet \quad \frac{1}{2}x^3 \\[6pt] \bullet \quad -2x^2 \\[6pt] \bullet \quad \frac{2}{3}x \\[6pt] \bullet \quad 1 \\ \end{array} \)
\(\\\)
Dabei können die Potenzfunktionen, ebenso wie quadratische Funktionen, in gestreckter oder gestauchter Form vorliegen.
Wie sieht nun der Graph von \(f\) aus?
\(\\[2em]\)
Graph der Polynomfunktion
Wir definieren die Potenzfunktion als
\( \quad \begin{array}{ r c l } g(x) & = & \frac{1}{2}x^3 \\[5pt] h(x) & = & -2x^2 \\[5pt] j(x) & = & \frac{2}{3}x + 1 \\ \end{array} \)
\(\\\)
Durch die Überlagerung, oder besser gesagt Addition, der Graphen der Potenzfunktionen ergibt sich der Verlauf des Graphen \(f\).
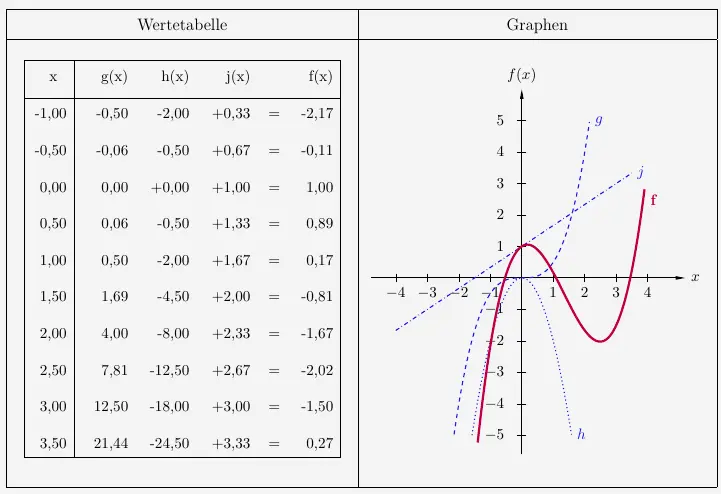
\(\\\)
Wie es für Polynomfunktionen typisch ist bilden sich Extrempunkte und Wendepunkte aus.
\(\\[2em]\)
Verlauf der ganzrationalen Funktionen
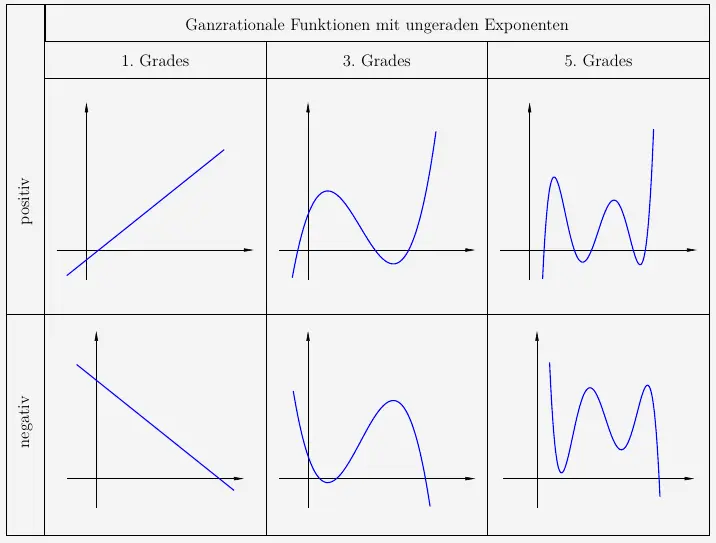
Ebenso wie Potenzfunktionen haben auch Polynome einen charakteristischen Kurvenverlauf, der durch den Grad, also dem Exponenten der Potenzfunktion des Polynoms mit dem höchsten Exponenten, bestimmt wird. Die Potenzfunktion mit dem höchsten Exponenten legt ebenfalls die Verlaufsrichtung fest.

\(\\\)
\(\\[2em]\)
Eigenschaften der Polynomfunktionen
Wie leicht zu erkennen ist, bilden sich hier die gleichen Verläufe wie bei den Potenzfunktionen.
Zusätzliche können sich aber (müssen sie jedoch nicht) noch Hoch- und Tiefpunkte herausbilden.
Man kann nun auch noch Aussagen über die maximal mögliche Anzahl der Nullstellen, Extrempunte und Wendepunkte machen.
Der Wertebereich ergänzt schließlich noch die Grenzwerte. Das heißt, dass untersucht wird, ob der Wertebereich Einschränkungen hat, also ob die Funktion tiefste/höchste Punkte (globales Minimum/globales Maximum) besitzt.
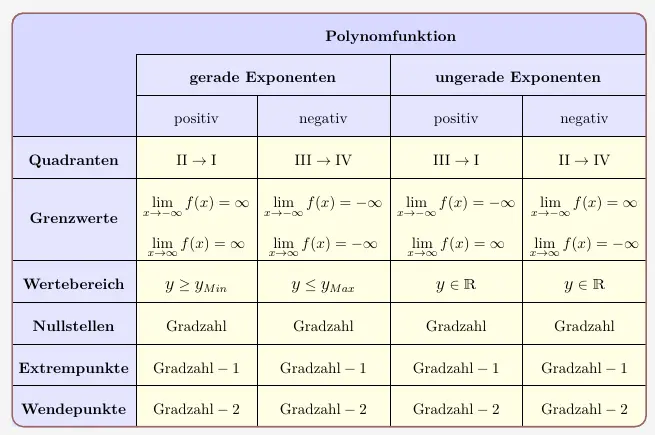
\(\\[2em]\)
Kurvendiskussion ganzrationaler Funktionen
Eine vollständige Kurvendiskussion ganzrationaler Funktionen enthält die Punkte
-
Allgemeine Untersuchung
- Definitionsbereich
- Symmetrie
- Verhalten im Unendlichen (Randuntersuchung)
\(\\\)
-
Konkrete Untersuchung
- Achsenschnittpunkte
- Ableitungen
- Extrempunkte
- Wendepunkte
\(\\\)
-
Abschließende Untersuchung
- Wertemenge
- Graph zeichnen
\(\\\)
Beispiel:
Die Kurvendiskussion wird anhand einer Funktion 3. Grades dargestellt.
\( \quad f(x) \; = \; 0{,}1 x^3 + 0{,}3 x^2 - 0{,}9 x \)
\(\\[1em]\)
1. Definitionsbereich
Bei allen ganzrationalen Funktion gilt, also auch hier,
\( \quad \mathbb{D} = \mathbb{R} \)
\(\\[1em]\)
2. Symmetrie
Da die ganzrationale Funktion aus achsensymmetrischen und punktsymmetrischen Potenzfunktionen besteht, ist keine eindeutige Symmetrie erkennbar.
Oder anders ausgedrückt:
Da sowohl gerade als auch ungerade Exponenten bei der Funktion vorhanden sind, ist die Funktion nicht symmetrisch.
\(\\[1em]\)
3. Verhalten im Unendlichen (Randuntersuchung)
Entsprechend dem Verlauf der ganzrationalen Funktionen
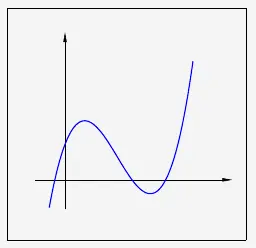
\(\\\)
und den Eigenschaften der Polynomfunktionen ist
\( \quad \lim \limits_{x \to -\infty} f(x) = -\infty \)
\(\\\)
und
\( \quad \lim \limits_{x \to \infty} f(x) = \infty \)
\(\\\)
Nun das Ganze rechnerisch. Für das Randverhalten
\( \quad \lim \limits_{x \to \pm \infty} f(x) \)
\(\\\)
kann bei ganzrationalen Funktionen nur \(\infty\) oder \(-\infty\) infrage kommen. Ausschlaggebend für den Grenzwert ist stets die Potenzfunktion mit dem größten Exponenten, in diesem Fall \(0{,}1 x^3\).
Es gilt nun
\( \quad \lim \limits_{x \to \infty} f(x) \; = \; \lim \limits_{x \to \infty} 0{,}1 x^3 \; = \; \infty \)
\(\\\)
Denn wenn \(x\) gegen \(\infty\) strebt, so strebt auch \(0{,}1 x^3\) und damit \(f(x)\) gegen \(\infty\).
Anders bei
\( \quad \lim \limits_{x \to -\infty} 0{,}1 x^3 \)
\(\\\)
Auch hier liegt \(x\) in der 3. Potenz vor. Das heißt, dass Minus wieder zu Minus wird. Wir erhalten also ein negatives Vorzeichen.
\( \quad \lim \limits_{x \to -\infty} f(x) \; = \; \lim \limits_{x \to -\infty} 0{,}1 x^3 \; = \; -\infty \)
\(\\[1em]\)
4. Achsenschnittpunkte
a) Schnittpunkt mit der Y-Achse
Es gilt: \(x=0\)
\( \quad f(0) \; = \; 0 \)
\(\\\)
Der Achsenabschnitt liegt bei \(S_y(0|0)\).
\(\\[1em]\)
b) Schnittpunkte mit der X-Achse (Nullstellen)
Für Nullstellen gilt: \(f(x)=0\)
\( \quad 0 \; = \; 0{,}1 x^3 + 0{,}3 x^2 - 0{,}9 x \)
\(\\\)
Kommen bei allen Termen einer ganzrationalen Gleichung, die Null ergibt, ein \(x\) vor, so wird \(x\) ausgeklammert.
\( \quad 0 \; = \; x \cdot \big( 0{,}1 x^2 + 0{,}3 x - 0{,}9 \big) \)
\(\\\)
Ergibt eine Multiplikation Null, so kann auch jeder Faktor Null ergeben (Nullprodukt).
\( \quad 0 \; = \; \underbrace{x}_{0} \cdot \big( \underbrace{ 0{,}1 x^2 + 0{,}3 x - 0{,}9 }_{0} \big) \)
\(\\\)
Wir machen jetzt eine Fallunterscheidung.
\(\\\)
1. Fall:
\( \quad x_1 \; = \; 0 \)
\(\\\)
Dies ist schon die erste Lösung.
\(\\\)
2. Fall:
\( \quad x_1 \; = \; 0{,}1 x^2 + 0{,}3 x - 0{,}9 \)
\(\\\)
Wir lösen mit der PQ-Formel.
\( \quad \begin{array}{ r c l l } 0 & = & 0{,}1 x^2 + 0{,}3 x - 0{,}9 & | \; \cdot 10 \\[5pt] 0 & = & x^2 + 3 x - 9 & \\[15pt] x_{2{,}3} & = & -\frac{p}{2} \pm \sqrt{ \left( \frac{p}{2} \right)^2 - q } \\[12pt] & = & -\frac{3}{2} \pm \sqrt{ \left( \frac{3}{2} \right)^2 - (-9) } \\[12pt] & = & -\frac{3}{2} \pm \sqrt{ \frac{9}{4} + \frac{36}{4} } \\[12pt] & = & -\frac{3}{2} \pm \sqrt{ \frac{45}{4} } \\[12pt] & = & -\frac{3}{2} \pm \frac{\sqrt{45}}{\sqrt{4} } \\[12pt] & = & -\frac{3}{2} \pm \frac{\sqrt{45}}{2} \\[12pt] x_2 & = & \frac{-3 + \sqrt{45}}{2} \\[6pt] x_2 & \approx & 1{,}85 \\[12pt] x_3 & = & \frac{-3 - \sqrt{45}}{2} \\[6pt] x_3 & \approx & -4{,}85 \\ \end{array} \)
\(\\\)
Die Nullstellen liegen also bei
\( \quad \begin{array}{ l } N_1( 0|0) \\[5pt] N_2( 1{,}85|0) \\[5pt] N_3( -4{,}85|0 ) \\ \end{array} \)
\(\\[1em]\)
5. Ableitungen
\( \quad \begin{array}{ r c l l } f'(x) & = & 0{,}3 x^2 + 0{,}6 x - 0{,}9 \\[5pt] f''(x) & = & 0{,}6 x + 0{,}6 \\[5pt] f'''(x) & = & 0{,}6 \\ \end{array} \)
\(\\[1em]\)
6. Extrempunkte
-
Notw. Bed.: \(f'(x) = 0\)
\( \quad \begin{array}{ r c l l } 0 & = & 0{,}3 x^2 + 0{,}6 x - 0{,}9 & | \; : 0{,}3 \\[5pt] 0 & = & x^2 + 2 x - 3 \\[15pt] x_{_{E_{1{,}2}}} & = & -\frac{p}{2} \pm \sqrt{ \left( \frac{p}{2} \right)^2 - q } \\[12pt] x_{_{E_{1{,}2}}} & = & -\frac{2}{2} \pm \sqrt{ \left( \frac{2}{2} \right)^2 - (-3) } \\[10pt] & = & -1 \pm \sqrt{ 1^2 + 3 } \\[5pt] & = & -1 \pm 2 \\[12pt] x_{_{E_{1}}}& = & \; \; \, 1 \\[5pt] x_{_{E_{2}}}& = & -3 \\ \end{array} \)
\(\\\)
-
Hinr. Bed.: \(f(x_{_{E}}) \not= 0\)
Wir überprüfen die Werte von \(x_{_{E}}\).
\( \quad \begin{array}{ r c c c r c l l } f''(1) & = & 0{,}6 \cdot 1 + 0{,}6 & = & 1{,}2 & > & 0 & \quad \Rightarrow \; \text{T} \\[6pt] f''(-3) & = & 0{,}6 \cdot (-3) + 0{,}6 & = & -1{,}2 & < & 0 & \quad \Rightarrow \; \text{H} \\ \end{array} \)
\(\\\)
-
Funktionswerte:
Bisher haben wir nur die \(x\)-Werte betrachtet. Für den \(y\)-Wert setzen wir die \(x\)-Werte in die Ausgangsfunktion ein.
\( \quad \begin{array}{ r c c c r } f(1) & = & 0{,}1\cdot 1^3 + 0{,}3 \cdot 1^2 - 0{,}9 \cdot 1 & = & - 0{,}5 \\[6pt] f(-3) & = & 0{,}1 \cdot (-3)^3 + 0{,}3 \cdot (-3)^2 - 0{,}9 \cdot (-3) & = & 2{,}7 \\ \end{array} \)
\(\\\)Damit erhalten wir den Tiefpunkt bei \(\text{T} (1|- 0{,}5 )\) und den Hochpunkt bei \(\text{H} (-3| 2{,}7 )\).
\(\\[1em]\)
7. Wendepunkte
-
Notw. Bed.: \(f''(x) = 0\)
\( \quad \begin{array}{ r c l l } 0 & = & 0{,}6 x + 0{,}6 & | \; - 0{,}6 x \\[5pt] -0{,}6 x & = & 0{,}6 & | \; (- 0{,}6) \\[5pt] x_{_{W}} & = & -1 \\ \end{array} \)
\(\\\)
-
Hinr. Bed.: \(f'''(x_{_{W}}) \not= 0\)
Wir überprüfen \(x_{_{W}}\).
\( \quad \begin{array}{ r c c c l l } f'''(-1) & = & 0{,}6 & > & 0 & \quad \Rightarrow \; \text{W} \\ \end{array} \)
\(\\\)
Ferner bedeutet \(f'''(-1) > 0\), dass bei \(x = -1\) ein Rechts-Links-Wechsel stattfindet.
\(\\\)
-
Funktionswerte:
\( \quad \begin{array}{ r c c c r } f(-1) & = & 0{,}1 \cdot (-1)^3 + 0{,}3 \cdot (-1)^2 - 0{,}9 \cdot (-1) & = & 1{,}1 \\ \end{array} \)
\(\\\)
Damit erhalten wir den Wendepunkt bei \(\text{W} (-1|1{,}1 )\).
\(\\[1em]\)
8. Wertemenge
Die Wertemenge gibt den Bereich der möglichen \(y\)-Werte an. Da
\( \quad \lim \limits_{x \to \infty} f(x) \; = \; \infty \)
\(\\\)
und
\( \quad \lim \limits_{x \to -\infty} f(x) \; = \; -\infty \)
\(\\\)
ist, und eine ganzrationalen Funktion \textcolor{blue}{stetig} ist, müssen auch alle Werte dazwischen existieren. Damit gilt
\( \quad \mathbb{W} \; = \; \mathbb{R} \)
\(\\[1em]\)
9. Graph zeichnen

\(\\[1em]\)