unabhängige Variable
Beschreibung der Variablen
Beispiel:
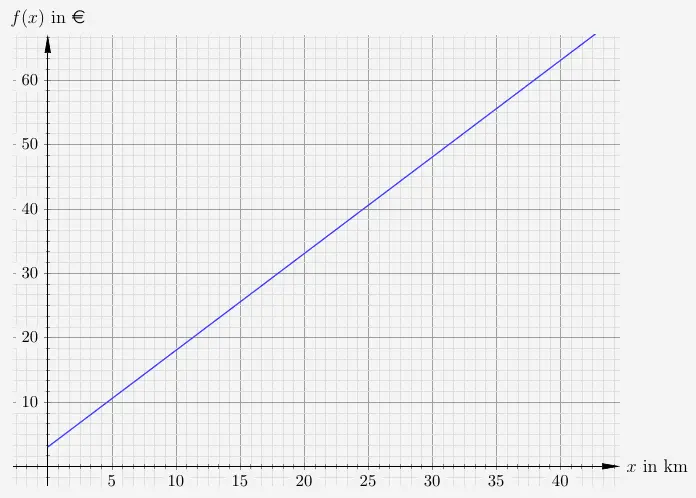
Ein Taxiunternehmen berechnet den Preis einer Taxifahrt mit 1,50 € pro km und einer Grundgebühr von 3 €.
\(\\\)
Der Preis einer Taxifahrt wird berechnet mit
\( \quad f(x) = 1{,}5x + 3 \)
\(\\\)
Dabei bezeichnen wir \(x\) als die unabhängige Variable und \(f(x)\) als die abhängige Variable, denn der Preis berechnet sich aus den gefahrenen Kilometern. Es heißt auch, dass \(f(x)\) eine Funktion von \(x\) ist.
\(\\[1em]\)
Ableitung mit mehreren Variablen
Eine Funktion wird stets nach der Variablen abgeleitet, von der sie abhängig ist. Das heißt, dass \(f(x)\) nach \(x\) und \(f(a)\) nach \(a\) abgeleitet wird.
Die anderen Variablen werden beim Ableiten wie Konstanten behandelt.
\( \quad \begin{array}{ r *{8}{c} } f(x) & = & ax^3y^2 & + & a^2x^2 & + & a^3bx & + & ay \\[6pt] f'(x) & = & 3ax^2y^2 & + & 2a^2 x & + & a^3b \\[24pt] f(a) & = & ax^3y^2 & + & a^2x^2 & + & a^3bx & + & ay \\[6pt] f'(a) & = & x^3y^2 & + & 2a x^2 & - & 3a^2bx & + & y \\[24pt] f(b) & = & ax^3y^2 & + & a^2x^2 & + & a^3bx & + & ay \\[6pt] f'(b) & = & a^3 x \\[24pt] f(y) & = & ax^3y^2 & + & a^2x^2 & + & a^3bx & + & ay \\[6pt] f'(y) & = & 2a x^3 y & + & a \\ \end{array} \)
\(\\[1em]\)