Potenzfunktionen mit positiven Exponenten
Inhaltsverzeichnis
\(\\\)
Potenzfunktionen sind unterteilt in Potenzfunktionen mit
- positiven Exponenten, aus denen die ganzrationale Funktionen hervorgehen,
- negativen Exponenten, aus denen die gebrochen-rationalen Funktionen hervorgehen.
\(\\\)
Die Graphen von Potenzfunktionen mit positiven Exponenten können in vier verschiedenen Verlaufsformen auftreten:
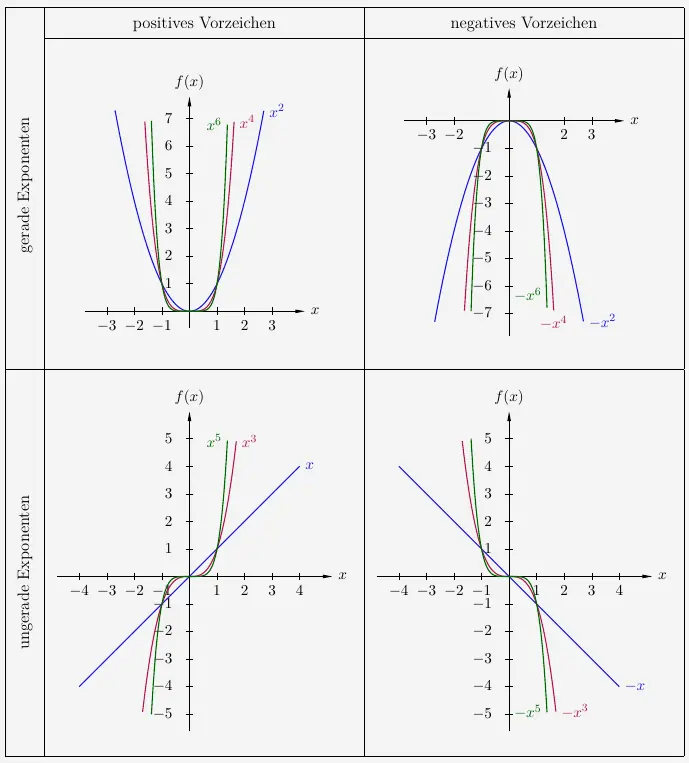
\(\\[2em]\)
Randverhalten
Die Verläufe der Potenzfunktionen lassen sich gut über ihr Verhalten am linken und rechten Rand der Funktionsgraphen charakterisieren. Dazu sehen wir uns die folgenden 2 Beschreibungsmethoden an.
\(\\[1em]\)
Quadranten des Koordinatensystems
Das Koordinatenkreuz lässt sich in 4 Bereiche aufteilen:
\( \quad \small \begin{array}{ r c l } \textrm{Quadrant I} & : & \textrm{positive x-Achse und positive y-Achse} \\[5pt] \textrm{Quadrant II} & : & \textrm{negative x-Achse und positive y-Achse} \\[5pt] \textrm{Quadrant III} & : & \textrm{negative x-Achse und negative y-Achse} \\[5pt] \textrm{Quadrant IV} & : & \textrm{positive x-Achse und negative y-Achse} \\ \end{array} \normalsize \)
\(\\\)
Das Ganze graphisch:
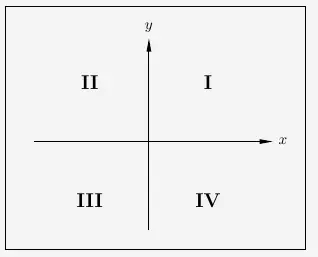
\(\\\)
Bei der Funktion \(f(x)=x^3\) verläuft der Graph,
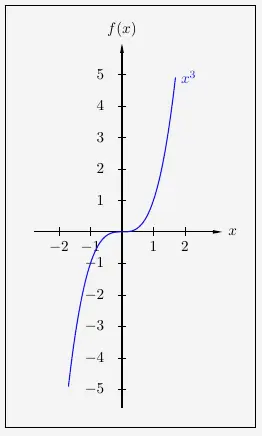
\(\\\)
von links nach rechts gesehen, von dem \(\textrm{III}\). Quadranten in den \(\textrm{I}\). Quadranten.
\(\\[1em]\)
Grenzwerte des Randverhaltens
Wir können auch sagen, dass der Graph, wenn wir an der linken Rand gehen, dann geht der Graph zum unteren Rand hin und wenn wir an den rechten Rand gehen, so geht der Graph zum oberen Rand hin.
Da es nun aber keinen Rand gibt, und der Graph in alle Richtungen ins nahezu Unendliche (Unendlich selbst ist für den Zahlenbereich der reellen Zahlen nicht definiert) geht, drücken wir es wie folgt aus:
Strebt \(x\) gegen \(-\infty\) , so geht \(f(x)\) auch gegen \(-\infty\).
Geschrieben:
\( \quad \lim \limits_{x \to -\infty} f(x) = -\infty \)
\(\\\)
Und in die andere Richtung gilt:
Strebt \(x\) gegen \(\infty\) , so geht \(f(x)\) auch gegen \(\infty\).
Geschrieben:
\( \quad \lim \limits_{x \to \infty} f(x) = \infty \)
\(\\[1em]\)
Randverhalten von Potenzfunktionen mit positiven Exponenten
Zusammengefasst ergeben sich folgende Verlaufsformen für Potenzfunktionen:

\(\\[1em]\)
Symmetrie
Potenzfunktionen mit positiven Exponenten sind von Natur aus symmetrisch. Es gilt, dass Potenzfunktionen mit
-
geraden Exponenten eine Achsensymmetrie aufweisen.
-
ungeraden Exponenten eine Punktsymmetrie aufweisen.
\(\\[1em]\)
Übersicht Potenzfunktionen mit positiven Exponenten
Es ergibt sich nun die vollständige Tabelle für Potenzfunktionen mit positiven Exponenten.

\(\\[1em]\)