Shortboard
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Funktionsterm von f
Zuerst die allgemeine Definition der Funktion \(f\).
Beachte: Der Mal-Punkt muss bei der Definition mitgeschrieben werden.

\(\\\)
Es gelten folgende Bedingungen:
\( \quad \begin{array}{ r c c c l } \text{größte Breite} & : & H( 1|0{,}25 ) & \Rightarrow & \; f(1)=0{,}25 \\[6pt] & & & \Rightarrow & f'(1)=0 \\[6pt] \text{Heckbreite} & : & P( 2| 0{,}1 ) & \Rightarrow & \; f(2)=0{,}1 \\[6pt] \text{Bugspitze} & : & S( 0| 0 ) & \Rightarrow & \; f(0)=0 \\ \end{array} \)
\(\\\)
In \(\boxed{Math1}\) verwenden wir das Werkzeug für Gleichungssysteme und drücken dreimal um vier Zeilen zu erhalten. Wir füllen es den obigen Gleichungen entsprechend aus.

\(\\\)
Die gesuchte Funktion lautet
\( \quad f(x)=0{,}05 \cdot x^3 - 0{,}35 \cdot x^2 + 0{,}55 \cdot x \)
\(\\[2em]\)
Aufgabe 2 – Bugbreite und Heckbreite
Wir definieren Funktion \(f\) neu

\(\\\)
und berechnen die Werte.

\(\\\)
Die Breite beträgt am Bug \(27{,}30795567 \, cm\) und am Heck \(34{,}02780113 \, cm\).
\(\\[2em]\)
Aufgabe 3 – Breite von 40 cm
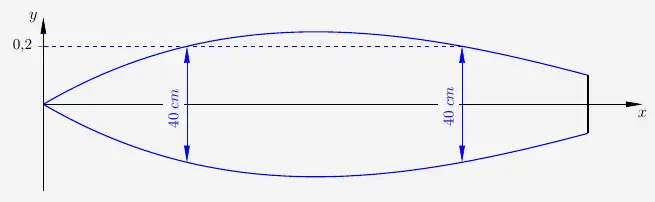
Für die Breite gilt
\( \quad f(x) \; = \; 0{,}2 \)
\(\\\)
Um die obige Gleichung zu lösen, verwenden wir den \(solve\)-Befehl. Diesen finden wir in \(\boxed{Math1}\) oder auch in \(\boxed{Math3}\).

\(\\\)
\(x=4{,}935432332\) liegt außerhalb des Definitionsbereichs. Damit ist die Breite
\( \quad 1{,}537401577 - 0{,}527166091 \; \approx \; 1{,}01 \, m \)
\(\\[2em]\)
Aufgabe 4 – Öffnungswinkel an der Bugspitze
Der halbe Öffnungswinkel befindet sich zwischen der \(x\)-Achse und der oberhalb liegenden Tangente. Für den Winkel \(\alpha\) gilt also
\( \quad tan\left( \frac{\alpha}{2} \right) \; = \; m \)
\(\\\)
Dabei ist \(m\) die Steigung dieser Tangente, die mit
\( \quad m \; = \; f'(0) \)
\(\\\)
berechnet wird. Für \(\alpha\) wählen wir die Variable \(a\) und berechnen diese. Hierbei ist zu beachten, dass der Classpad auf Grad, also 360° eingestellt ist.

\(\\\)
Die Tangensfunktion ist eine periodische Funktion, so dass es unendlich viele Lösungen gibt. Mit einem geeigneten \(constn(1)\), in diesem Fall scheint \(constn(1)=0\) günstig zu sein, erhalten wir
\( \quad \alpha \; = \; 360 \cdot 0 + 57{,}62158749 \; \approx \; 57{,}62^\circ \)
\(\\[2em]\)
Aufgabe 5 – Volumen des Surfbretts

\(\\\)
Das Volumen des Surfbretts wird berechnet mit
\( \quad V \; = \; Fl\ddot{a}che \; der \; Oberseite \times H\ddot{o}he \; des \; Surfbretts \)
\(\\\) Dabei kann die Oberseite mit dem Integral berechnet werden.

\(\\\)
Das Volumen beträgt \(0{,}03666666667 \, m^3 \cdot 1000 \frac{l}{m^3} \; \approx \; 36{,}67 \, l\).
\(\\\)