Verschieben von Funktionen
Inhaltsverzeichnis
\(\\\)
Funktionen können nach links oder rechts und nach oben oder unten verschoben werden. Wir betrachten nun dies bei ganzrationalen Funktionen, e-Funktionen und trigonometrischen Funktionen. Am Besten kann man die Verschiebung bei trigonometrischen Funktionen veranschaulichen.
\(\\[1em]\)
1. Verschieben von trigonometrischen Funktionen
Verschieben in x-Richtung von trigonometrischen Funktionen
Bei der allgemeinen Gleichung der trigonometrischen Funktionen
\( \quad f(x) \; = \; a \cdot sin \big( b \cdot (x - c) \big) + d \)
\(\\\)
ist der Parameter \(c\) verantwortlich für die Verschiebung des Graphen in \(x\)-Richtung.
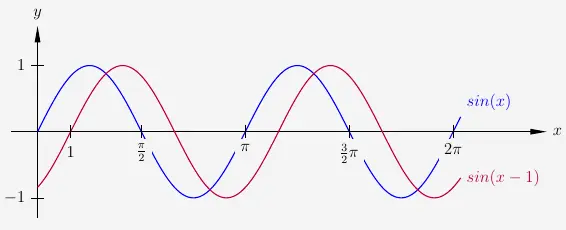
Dabei ist zu beachten, dass in der allgemeinen Gleichung \(x - c\) steht, was dann auch so notiert werden muss. Das heißt, dass bei einer Verschiebung um \(1\) Einheit nach rechts muss die verschobene Funktion
\( \quad f(x) \; = \; sin(x - 1) \)
\(\\\)
lauten und bei einer Verschiebung um \(1\) Einheit nach links
\( \quad f(x) \; = \; sin\big(x - (-1)\big) \; = \; sin(x + 1) \)
\(\\[2em]\)
Verschieben in y-Richtung von trigonometrischen Funktionen
Verschieben wir weiter die obige Funktion zu einer Funktion \(g\) um 2 Einheiten nach oben,
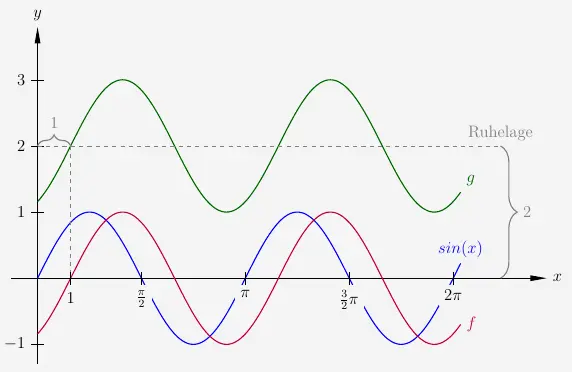
so entsteht nach der allgemeinen Gleichung, wobei der Parameter \(d\) die Höhenverschiebung angibt,
\(\quad f(x) \; = \; sin(x - 1) + 2 \)
\(\\[2em]\)
2. Verschieben von e-Funktionen
Eine gestreckte und gestauchte und verschobene \(e\)-Funktion ist allgemein von der Form
\( \quad f(x) \; = \; a \cdot e^{b \cdot (x - c)} +d \)
\(\\\)
Dabei geben \(c\) und \(d\) entsprechend der trigonometrischen Funktionen die Verschiebungen an.
\(e^x\) sei um \(0{,}5\) Einheiten nach rechts und \(1\) Einheit nach oben verschoben.
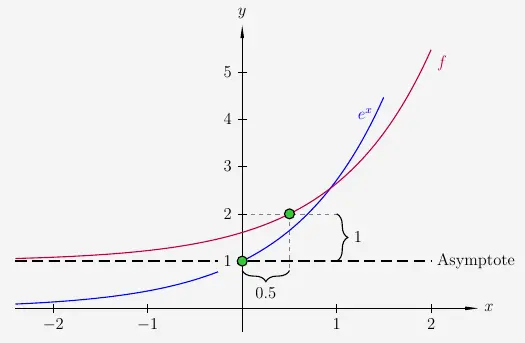
Aus den Verschiebungen ergibt sich die Funktion \(f\) mit der Funktionsgleichung
\(\quad f(x) \; = \; e^{x - 0{,}5} +1 \)
\(\\[2em]\)
3. Verschieben von ganzrationalen Funktionen
Entsprechend der Verschiebung trigonometrischer Funktionen werden ganzrationale Funktionen verschoben.
Ganzrationale Funktionen können als die Summe von Potenzfunktionen aufgefasst werden.
Deren Verschiebung werden auf folgende Weise notiert:
\(\\[1em]\)
Seitliche Verschiebung von Potenzfunktionen

Beachte:
Bei Verschiebung in x-Richtung müssen wir immer das umgekehrte Vorzeichen nehmen.
\(\\[2em]\)
Höhenverschiebung von Potenzfunktionen
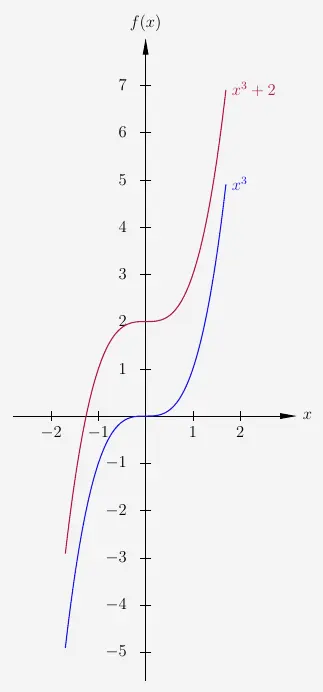
Hier ist für den roten Graphen jeder Punkt des blauen Graphen um 2 erhöht, auch wenn es auf dem ersten Blick nicht ganz so scheint.
\(\\[2em]\)
Verschiebung von Polynomen
Die Verschiebung wird nun angewendet auf ein Polynom, zusammengesetzt aus mehreren Potenzfunktionen, mit beispielsweise einer Funktion \(f\) ,
\( \quad f(x) \; = \; 0{,}25x^3 - 1{,}5x^2 + 0{,}75x + 2{,}5 \)
\(\\\)
die um \(2\) Einheiten nach rechts und \(1{,}5\) Einheiten nach oben versetzt wird.

Es ergibt sich eine Funktion \(g\) mit
\( \quad g(x) \; = \; 0{,}25 \cdot (x-2)^3 - 1{,}5 \cdot (x-2)^2 + 0{,}75 \cdot (x-2) + 4 \)
\(\\\)
Beachte: Jeder \(x\)-Wert erhält die gleiche Verschiebung.
\(\\[1em]\)