Basiswissen Parabel
Inhaltsverzeichnis
\(\\\)
Allgemeine Gleichung einer quadratischen Funktion
In der Regel liegt eine quadratische Gleichung in der allgemeinen Form
\( \quad f(x) \, = \, ax^2 + bx + c \)
\(\\\)
vor. Dabei gibt \(a\) den Streckungsfaktor und \(c\) den Achsenabschnitt an. Dem Parameter \(b\) kann erst nach Umformung, siehe Scheitelpunktform, eine eindeutige Bedeutung zugemessen werden.
Der Graph einer quadratischen Funktion stellt eine Parabel dar. Bei dieser sind die Nullstellen von besonderer Bedeutung und werden in einem Extrabeitrag behandelt.
\(\\[2em]\)
Eigenschaften von Parabeln
Normalparabel
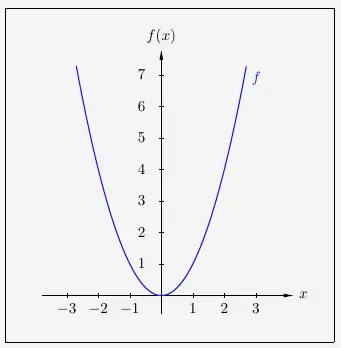
Den Graphen der Funktion \(f\) mit
\( \quad f(x) \, = \, x^2 \)
\(\\\)
bezeichnet man als Normalparabel.
\(\\\)
Die Normalparabel ist symmetrisch zur \(y\)-Achse und hat den Scheitelpunkt im Koordinatenursprung.
\(\\[1em]\)
Streckung und Stauchung einer Parabel
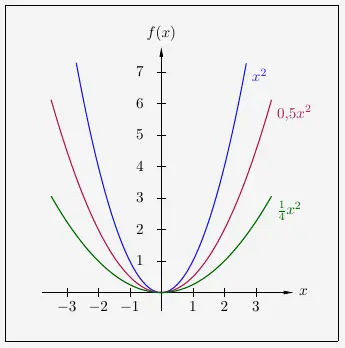
In der Form
\( \quad f(x) \, = \, ax^2 \)
\(\\\)
gibt a den Streckungsfaktor an.
\(\\\)
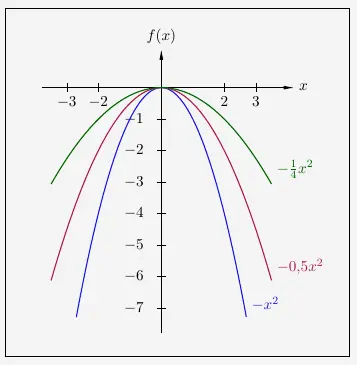
Ist der Streckungsfaktor negativ, so sind die Parabeln nach unten geöffnet.
\(\\\)
Ist der \(|a|\) größer als 1, so heißt die Parabel gestreckt. Das heißt, dass die Parabel schmaler als die Normalparabel ist.
Liegt der \(|a|\) zwischen 0 und 1, so heißt die Parabel gestaucht. Das heißt, dass die Parabel breiter als die Normalparabel ist.
\(\\[1em]\)
Verschiebung der Parabel
Verschiebung in der Höhe
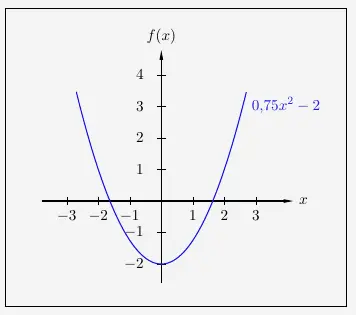
In der Form
\( \quad f(x) \, = \, ax^2 + c \)
\(\\\)
gibt \(c\) die Verschiebung der Parabel nach oben oder unten und damit auch den Achsenabschnitt (Durchgang durch die \(y\)-Achse) an.
\(\\[1em]\)
Seitliche Verschiebung
In der Form
\( \quad f(x) \, = \, (x -d)^2 \) \(\\\)
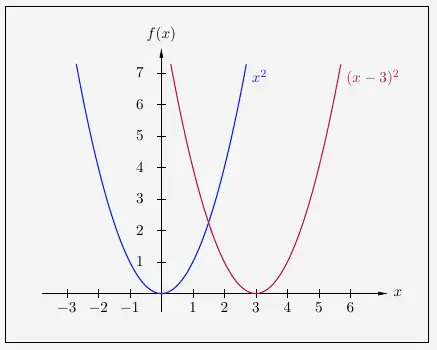
gibt \(d\) die Verschiebung der Parabel in \(x\)-Richtung an. Zu beachten ist, dass eine Verschiebung um 3 Einheiten nach rechts mit
\( \quad f(x) \, = \, (x -3)^2 \)
\(\\\)
notiert wird.
\(\\\)
Die Kombination von Höhenverschiebung und seitlicher Verschiebung der Parabel wird in dem Kapitel Scheitelpunktform einer quadratischen Funktion behandelt.
\(\\[1em]\)