Aufgaben
Inhaltsverzeichnis
\(\\\)
“Körper”
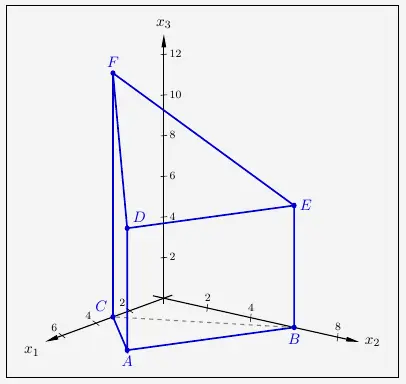
Die Abbildung zeigt den Körper \(ABCDEF\) mit
\( \quad A(6|3|0)\), \(B(0|6|0)\), \(C(3|0|0)\), \(D(6|3|6)\), \(E(0|6|6)\) und \(F(3|0|12)\).
\(\\\)
\(\qquad \qquad\)
\(\\[1em]\)
Ebene L
- Untersuchen Sie, ob das Dreieck \(DEF\) gleichschenklig ist.
(4 P)
\(\\\)
-
Die Punkte \(D\), \(E\) und \(F\) liegen in einer Ebene \(L\). Ermitteln Sie eine Gleichung von \(L\) in Koordinatenform.
\(\quad \big[ \text{Zur Kontrolle:} \quad L: 2x_1 + 4x_2 + 3x_3 - 42 = 0 \big]\)
(4 P)
\(\\\)
- Bestimmen Sie die Größe des Winkels, den \(L\) mit der \(x_1x_2\)-Ebene einschließt.
(3 P)
\(\\\)
- Berechnen Sie den Abstand des Ursprungs zur Ebene \(L\).
(3 P)
\(\\\)
- Bestimmen Sie eine Gleichung der Schnittgeraden von \(L\) mit der \(x_1x_2\)-Ebene in Parameterform.
(3 P)
\(\\[2em]\)
Flächen und Volumen
- Begründen Sie, dass das Viereck \(ADFC\) ein Trapez ist.
(2 P)
\(\\\)
-
Der Flächeninhalt des Dreiecks \(ABC\) kann mit dem Term
\( \quad 6 \cdot 6 - \frac{1}{2} \cdot 3 \cdot 3 -2 \cdot \frac{1}{2} \cdot 3 \cdot 6 \)
berechnet werden. Veranschaulichen Sie diese Tatsache durch geeignete Eintragungen auf dem Arbeitsblatt.
(6 P)
\(\\\)
- Berechnen Sie das Volumen des Körpers \(ABCDEF\).
(3 P)
\(\\\)
- Auf der Kante \(\overline{AD}\) liegt der Punkt \(Q\), auf der Kante \(\overline{BE}\) der Punkt \(R(0|6|2)\). Das Dreieck \(FQR\) hat in \(Q\) einen rechten Winkel.
Bestimmen Sie die \(x_3\)-Koordinate von \(Q\).(5 P)
\(\\[2em]\)
Ebene \(N_k\)
Die Ebene \(N_k\) enthält die \(x_3\)-Achse und den Punkt \(P_k(1-k|k|0)\) mit \(0<k<1\).
\(\\\)
-
Für einen bestimmten Wert \(k\) besitzt \(N_k\) die Gleichung
\( \quad -3x_1 + 6x_2 = 0 \).
Zeichnen Sie die Schnittfläche dieser Ebene mit dem Körper \(ABCDEF\) auf dem Arbeitsblatt ein.
(3 P)
\(\\\)
-
Welche Kanten des Körpers von \(N_k\) geschnitten werden, ist abhängig von \(k\)
Durchläuft \(k\) alle Werte zwischen \(0\) und \(1\), so gibt es Bereiche \(]a;b[\), für die \(N_k\) für alle Werte von \(k\) mit \(a<k<b\) jeweils die gleichen Kanten des Körpers schneidet. Bestimmen Sie den größten dieser Bereiche und geben Sie die zugehörige Kanten an.
(4 P)
\(\\[2em]\)
Aufgabenstellung formulieren
Der Körper wird so um die Gerade \(AB\) gedreht, dass der vor der Drehung mit \(D\) bezeichnete Eckpunkt nach der Drehung in der \(x_1x_2\)-Ebene liegt und dabei eine positive \(x_2\)-Koordinate hat. Die folgenden Rechnungen liefern die Lösung einer Aufgabe im Zusammenhang mit der beschriebenen Drehung.
\( \quad \overrightarrow{BA} \circ \left[ \overrightarrow{OB} + r \cdot \overrightarrow{BA} - \overrightarrow{OC} \right] = 0 \quad \Longleftrightarrow \quad r = 0{,}8 \)
\(\\\)
Mit
\(\overrightarrow{OS} = \overrightarrow{OB} + r \cdot \overrightarrow{BA} \;\) folgt \(\; S(4{,}8|3{,}6|0)\).
\(\\\)
\( \overrightarrow{OT} = \overrightarrow{OS} + \bigl| \overrightarrow{CS} \bigl| \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right) \end{smallmatrix} \)
\(\\\)
Formulieren Sie eine passende Aufgabenstellung und geben Sie die Bedeutung von \(S\) an.
(3 P)
\(\\[1em]\)