HMF 7 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Punkt A
Zunächst benötigen wir \(g\) mit
\( \quad \overrightarrow{x} = \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right) \end{smallmatrix} +r \cdot \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 2 \\ 2 \end{array} \right) \end{smallmatrix} \)
\(\\\)
Wir machen die Punktprobe mit \(A(3|5|5)\).
\( \quad \begin{array}{r c l l l } \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 5 \\ 5 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right) \end{smallmatrix} +r \cdot \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 2 \\ 2 \end{array} \right) \end{smallmatrix} && \Biggl| \; - \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right) \end{smallmatrix} \\[12pt] \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 4 \\ 4 \end{array} \right) \end{smallmatrix} & = & r \cdot \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 2 \\ 2 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Es lässt sich leicht erkennen, das \(r=2\) ist. Damit liegt \(A\) auf der Geraden \(g\).
\(\\[2em]\)
Aufgabe 2 – Raute ABCD
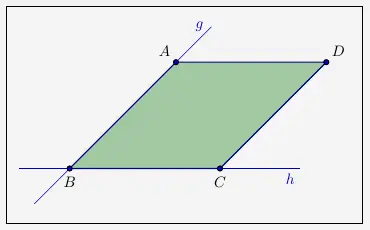
Eine Raute ist ein Parallelogramm mit gleich langen Seiten. Punkt \(C\) muss also von \(B\) genauso weit entfernt sein wie \(A\) von \(B\). Wir berechnen zunächst die Länge der Strecke \(\overline{BA}\).
\( \quad \begin{array}{ r c l c l c l } |\overrightarrow{BA}| & = & |\overrightarrow{a} - \overrightarrow{b}| & = & \begin{vmatrix} \left[ \begin{smallmatrix} \left( \begin{array}{r} 3 \\ 5 \\ 5 \end{array} \right) - \left( \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right) \end{smallmatrix} \right] \end{vmatrix} & = & \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} 2 \\ 4 \\ 4 \end{array} \right) \end{smallmatrix} \end{vmatrix} \\[12pt] & & & = & \sqrt{2^2 + 4^2 + 4^2} \\[6pt] & & & = & \sqrt{4 + 16 + 16} \\[6pt] & & & = & \sqrt{36} \\[6pt] & & & = & 6 \end{array} \)
\(\\\)
Punkt \(C\) ist also \(6\) Einheiten von Punkt \(B\) entfernt und liegt auf der Geraden \(h\) mit
\( \quad \overrightarrow{x} = \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right) \end{smallmatrix} +s \cdot \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} \)
\(\\\)
Da der Richtungsvektor von \(h\) genau die Länge
\( \quad \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} \end{vmatrix} =1 \)
\(\\\)
hat, ergibt sich der Vektor \(\overrightarrow{c}\) mit
\( \quad \overrightarrow{c} = \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right) \end{smallmatrix} +6 \cdot \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} = \begin{smallmatrix} \left( \begin{array}{c} 7 \\ 1 \\ 1 \end{array} \right) \end{smallmatrix} \)
\(\\\)
Für den Punkt \(D\) gilt die Linearkombination
\( \quad \begin{array}{ r c l } \overrightarrow{d} & = & \overrightarrow{c} + \overrightarrow{CD} \\[8pt] & = & \overrightarrow{c} + \overrightarrow{BA} \\[8pt] & = & \begin{smallmatrix} \left( \begin{array}{c} 7 \\ 1 \\ 1 \end{array} \right) \end{smallmatrix} + \begin{smallmatrix} \left( \begin{array}{r} 2 \\ 4 \\ 4 \end{array} \right) \end{smallmatrix} \\[10pt] & = & \begin{smallmatrix} \left( \begin{array}{c} 9 \\ 5 \\ 5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Damit ergeben sich die Punkte \(C(6|1|1)\) und \(D(9|5|5)\) für die Raute \(ABCD\).
\(\\[1em]\)