Flächen und Volumen
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Trapez
Laut Definition ist ein Trapez ein (ebenes) Viereck, bei dem zwei Seiten parallel zueinander sind. Die anderen beiden Seiten brauchen nicht parallel zueinander liegen. Falls sie es doch tun, liegt sogar ein Parallelogramm vor.
\( \quad \left. \begin{array}{ r c c c c c c } \overrightarrow{AD} & = & \overrightarrow{d} - \overrightarrow{a} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \\[10pt] \overrightarrow{CF} & = & \overrightarrow{f} - \overrightarrow{c} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{3} \\ \scriptstyle{0} \\ \scriptstyle{12} \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{3} \\ \scriptstyle{0} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{12} \end{array} \right) \end{smallmatrix} \end{array} \right\} \; \Rightarrow \; \textit{kollinar mit} \quad \overrightarrow{CF} = 2 \cdot \overrightarrow{AD} \)
\(\\\)
\( \quad \left. \begin{array}{ r c c c c c c } \overrightarrow{AC} & = & \overrightarrow{c} - \overrightarrow{a} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{3} \\ \scriptstyle{0} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{-3} \\ \scriptstyle{-3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} \\[10pt] \overrightarrow{DF} & = & \overrightarrow{f} - \overrightarrow{d} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{3} \\ \scriptstyle{0} \\ \scriptstyle{12} \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{-3} \\ \scriptstyle{-3} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \end{array} \right\} \; \Rightarrow \; \textit{nicht kollinar, denn} \quad \overrightarrow{DF} \not= t \cdot \overrightarrow{AC} \\ \)
\(\\\)
Sind die Vektoren \(\overrightarrow{AD}\) und \(\overrightarrow{CF}\) kollinear, so sind die Seiten \(\overline{AD}\) und \(\overline{DF}\) parallel zueinander. Damit ist das Viereck \(ADFC\) ein Trapez.
\(\\[2em]\)
Aufgabe 2 – Dreieck ABC
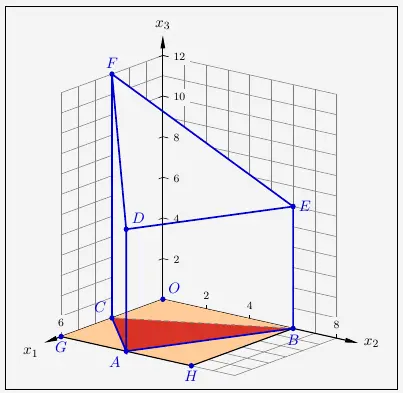
Das Viereck \(HBOG\) ist ein Quadrat mit der Kantenlänge \(6\). Ziehen wir davon die Dreiecke \(ACG\), \(ABH\) und \(OBC\) ab, so erhalten wir den Flächeninhalt des Dreiecks \(ABC\). Dabei gilt, dass die Fläche des Dreiecks
-
\(ACG\) berechnet wird mit \(\frac{1}{2} \cdot 3 \cdot 3\).
-
\(ABH\) berechnet wird mit \(\frac{1}{2} \cdot 3 \cdot 6\).
-
\(OBC\) berechnet wird mit \(\frac{1}{2} \cdot 3 \cdot 6\).
\(\\\)
Daraus resultiert die Fläche des Dreiecks \(ABC\) mit
\( \quad A \; = \; 6 \cdot 6 - \frac{1}{2} \cdot 3 \cdot 3 - 2 \cdot \frac{1}{2} \cdot 3 \cdot 6 \)
\(\\[2em]\)
Aufgabe 3 – Volumen des Körpers ABCDEF
Der Körper \(ABCDEF\) besteht aus einem geraden Prisma mit der Grundfläche \(G\) und der Höhe \(6\) und einer schiefen Pyramide mit der Grundfläche \(G\) und der Höhe von ebenfalls \(6\).
Die Grundfläche \(G\) berechnet sich aus den Dreiecke \(ABC\) und \(OBC\) mit
\( \quad G \; = \; 6 \cdot 6 - \frac{1}{2} \cdot 3 \cdot 3 - 2 \cdot \frac{1}{2} \cdot 3 \cdot 6 \; = \; 13{,}5 \)
\(\\\)
Das Volumen des Prismas erhalten wir mit
\( \quad V_{Prisma} \; = \; G \cdot h_{Prisma} \; = \; 13{,}5 \cdot 6 \; = \; 81 \)
\(\\\)
Das Volumen der Pyramide erhalten wir mit
\( \quad V_{Pyramide} \; = \; \frac{1}{3} \cdot G \cdot h_{Pyramide} \; = \; \frac{1}{3} \cdot 13{,}5 \cdot 6 \; = \; 27 \)
\(\\\)
Das Volumen des Körpers beträgt also
\( \quad V \; = \; 81 + 27 \; = \; 108 \, \textit{VE} \)
\(\\[2em]\)
Aufgabe 4 – Punkt Q
Sei das Dreieck \(FQR\) die Schnittfläche des Körpers. Dann stellt sich dieses folgendermaßen dar:

\(\\\)
Laut Aufgabenstellung liegt in \(Q\) ein rechter Winkel. Es muss also gelten:
\( \quad \overrightarrow{QF} \circ \overrightarrow{QR} \; = \; 0 \)
\(\\\)
Wir legen zunächst den Ortsvektor von \(Q\) fest mit
\( \quad \begin{array}{ r c l } \overrightarrow{q} & = & \overrightarrow{a} + t \cdot \overrightarrow{AD} \\[6pt] & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
und verwenden diesen in der Orthogonalitätsbedingung.
\( \quad \begin{array}{ r c l } \overrightarrow{QF} \circ \overrightarrow{QR} & = & 0 \\[6pt] \left(\overrightarrow{f} - \overrightarrow{q} \right) \circ \left(\overrightarrow{r} - \overrightarrow{q} \right) & = & 0 \\[6pt] \left[ \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{3} \\ \scriptstyle{0} \\ \scriptstyle{12} \end{array} \right) \end{smallmatrix} - \left( \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \right) \right] \circ \left[ \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{6} \\ \scriptstyle{2} \end{array} \right) \end{smallmatrix} - \left( \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \right) \right] & = & 0 \\[12pt] \left[ \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{3} \\ \scriptstyle{0} \\ \scriptstyle{12} \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} - t \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \right] \circ \left[ \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{6} \\ \scriptstyle{2} \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} - t \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \right] & = & 0 \\[12pt] \left[ \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{-3} \\ \scriptstyle{-3} \\ \scriptstyle{12} \end{array} \right) \end{smallmatrix} - t \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \right] \circ \left[ \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{-6} \\ \scriptstyle{3} \\ \scriptstyle{2} \end{array} \right) \end{smallmatrix} - t \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \right] & = & 0 \\ \end{array} \)
\(\\\)
Aufgelöst ergibt das Skalarprodukt
\( \quad \begin{array}{ r c l } -3 \cdot (-6) - 3 \cdot 3 + (12 - 6t) \cdot (2 -6t) & = & 0 \\[6pt] 18 - 9 + 24 -72t -12t +36t^2 & = & 0 \\[6pt] 36t^2 - 84t + 33 & = & 0 \\[10pt] t_1 & = & 1{,}833 \\[6pt] t_2 & = & 0{,}5 \\ \end{array} \)
\(\\\)
Da \(Q\) zwischen \(A\) und \(D\) liegen muss, kann \(t\) nur ein Wert im Intervall \([0;1]\) sein. Folglich ist \(t=0{,}5\).
Es ergibt sich \(\overrightarrow{q}\) mit
\( \quad \begin{array}{ r c l } \overrightarrow{q} & = & \overrightarrow{a} + t \cdot \overrightarrow{AD} \\[6pt] & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} + 0{,}5 \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{0} \\ \scriptstyle{6} \end{array} \right) \end{smallmatrix} \\[8pt] & = & \begin{smallmatrix} \left( \begin{array}{c} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{3} \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\\)
Damit ist vom Punkt \(Q\) die gesuchte Koordinate \(x_3 = 3\).
\(\\[1em]\)