Aufgaben
Inhaltsverzeichnis
\(\\\)
“Weckton (CAS)”
Gegeben ist die Schar der in \(\mathbf{R}\) definierten Funktion \(f_a\) mit
\( \quad f_a(x) \; = \; e^x \cdot (x-a)^2 \quad \text{mit } \, a \in \mathbf{R} \)
\(\\\)
Der Graph von \(f_a\) wird mit \(G_a\) bezeichnet. Jeder Graph der Schar hat genau einen Hochpunkt und genau einen Tiefpunkt. Die Abbildung 1 zeigt \(G_{\frac{3}{2}}\).

\(\\[1em]\)
Graph von \(G_a\)
\(\\\)
-
\(G_{\frac{3}{2}}\) nimmt in einem seiner Wendepunkte seine kleinste Steigung an.
Bestimmen Sie diese Steigung rechnerisch.
(4 P)
\(\\\)
-
\(G_a\) hat mit jeder der beiden Koordinatenachsen genau einen gemeinsamen Punkt. Geben Sie die Koordinaten dieser Punkte an.
Begründen Sie anhand des Funktionsterms, dass der gemeinsame Punkt mit der \(x\)-Achse der Tiefpunkt von \(G_a\) ist.
(3 P)
\(\\\)
-
Es gibt einen positiven Wert von \(a \,\), für den \(G_a\) und die Koordinatenachsen eine Fläche mit dem Inhalt \(3\) einschließen.
Bestimmen Sie diesen Wert von \(a\).
(3 P)
\(\\\)
-
Für jeden Wert von \(a\) mit \(a \not= 0\) schließt die Gerade durch die beiden Extrempunkte von \(G_a\) mit den Koordinatenachsen ein Dreieck ein.
Berechnen Sie denjenigen Wert von \(a \,\), für den dieses Dreieck gleichschenklig ist.
(5 P)
\(\\[2em]\)
Schar von \(f_{a,b}\)
Betrachtet wird die Schar der in \(\mathbf{R}\) definierten Funktionen \(f_{a,b}\) mit
\( \quad f_{a,b}(x) \; = \; e^x \cdot \big((x-a+b)^2 - b\big) \quad \text{mit } \, a,b \in \mathbf{R} \)
\(\\\)
Es gilt \(f_{a,0}(x) \; = \; f_a(x)\). Der Graph von \(f_{a,b}\) wird mit \(G_{a,b}\) bezeichnet.
\(\\[1em]\)
-
Für positive Werte von \(b\) hat \(G_{a,b}\) zwei Schnittpunkte mit der \(x\)-Achse. Für jeden Wert von \(a\) wird der Abstand dieser beiden Schnittpunkte betrachtet.
Zeigen Sie rechnerisch, dass dieser Abstand unabhängig von \(a\) ist.
(3 P)
\(\\\)
Erhöht man im Term von \(f_{a,b}\) den Wert \(b\) um \(1\), so erhält man einen Term der ersten Ableitungsfunktion von \(f_{a,b}\). Es gilt also
\( \quad f'_{a,b}(x) \; = \; f_{a,b+1}(x) \).
\(\\\)
-
Die Abbildung 2 zeigt für einen bestimmten Wert von \(a\) die Graphen zweier Funktionen der Schar, bei denen sich die Werte von \(b\) um \(1\) unterscheiden. Entscheiden Sie, welcher der beiden Graphen \(\textrm{I}\) und \(\textrm{II}\) zum größeren Wert von \(b\) gehört, und begründen Sie Ihre Entscheidung.

(3 P)
\(\\\)
-
Für jeden Wert von \(a\) gilt
\( \quad f_{a,0}(a) \; = \; 0 \)
und
\( \quad f_{a,1}(a) \; = \; 0 \)
und
\( \quad f_{a,2}(a) \; \not= \; 0. \)
\(\\\)
Geben Sie die Bedeutung dieser Tatsache für die Graphen der Funktionen \(f_{a,-1}\) an.
(3 P)
\(\\[2em]\)
Schalldruckpegel
Der Schalldruckpegel (im Folgenden vereinfacht als Lautstärke bezeichnet) von Wecktönen kann durch Funktionen beschrieben werden.
Die Lautstärke eines bestimmten Wecktons wird durch die in \([0;4]\) definierten Funktion \(h\) mit
\( \quad h(x) = \left\{ \begin{array}{ l l } -8x^2 + 25x & \text{für } \, 0 \leq x \leq 2 \\[5pt] -8x^2 + 57x -64 & \text{für } \, 2 < x \leq 4 \\ \end{array} \right. \)
\(\\\)
beschrieben. Dabei ist \(x\) die seit Beginn des Wecktons vergangene Zeit in Sekunden und \(h(x)\) die Lautstärke in Dezibel. Die Abbildung 3 zeigt einen Teil des Graphen von \(h\).
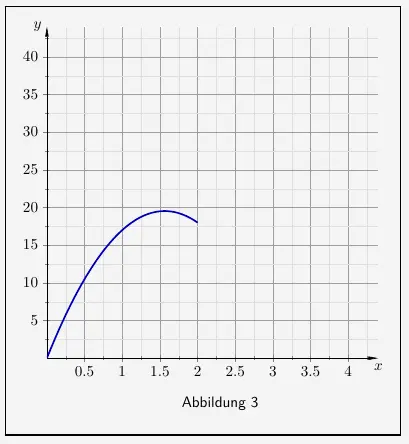
\(\\\)
- Zeigen Sie, dass der Graph von \(h\) bei \(x=2\) keinen Sprung aufweist, und vervollständigen Sie den Graphen in Abbildung 3.
(4 P)
\(\\\)
- Berechnen Sie den Zeitpunkt, zu dem der Weckton die größte Lautstärke hat, und geben Sie diese Lautstärke an.
(4 P)
\(\\\)
-
Berechnen Sie unter Verwendung der folgenden Information die durchschnittliche Lautstärke des Wecktons.
Der durchschnittliche Funktionswert von \(h\) im Intervall \([a;b]\) stimmt mit der Höhe eines Rechtecks überein, das die beiden folgenden Eigenschaften hat:
-
Das Rechteck hat die Breite \(\; b-a\)
-
Das Rechteck hat den gleichen Inhalt wie die Fläche, die für
\( \qquad a \leq x \leq b \)
\(\quad\) zwischen dem Graphen von \(h\) und der \(x\)-Achse liegt.
(4 P)
-
\(\\\)
-
Dem Graphen von \(h\) ist zu entnehmen, dass der Weckton innerhalb der ersten zwei Sekunden bestimmte Lautstärken zweimal annimmt. Zwei Zeitpunkte mit gleicher Lautstärke haben jeweils einen bestimmten Abstand.
Bestimmen Sie rechnerisch den größten dieser Abstände.
(4 P)
\(\\[2em]\)