Aufgaben

---

\(\\\)

“Drei Glücksspiele”

Alle in Ihren Lösungen verwendeten Zufallsgrößen müssen explizit eingeführt werden. Machen Sie auch Angaben über die Verteilung der jeweiligen Zufallsgrößen.

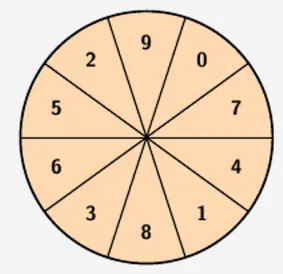
Die Sektoren des abgebildeten Glücksrads sind gleich groß und mit den Zahlen von \(0\) bis \(9\) durchnummeriert.

\(\\[1em]\)

Glücksrad drehen

1. Das Glücksrad wird zwanzigmal gedreht. Bestimmen Sie die Wahrscheinlichkeit der Folgenden Ereignisse \(A\), \(B\) und \(C\).

   \(\mathbf{\color{green}{A}}\)   ‘’Es wird genau siebenmal eine ungerade Zahl erzielt.‘’

   \(\mathbf{\color{green}{B}}\)   ‘’Es wird weniger als neunmal eine ungerade Zahl erzielt.‘’

   \(\mathbf{\color{green}{C}}\)   ‘’Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt.‘’

   (5 P)

\(\\\)

2. Das Glücksrad wird zweimal gedreht. Untersuchen Sie, ob die Ereignisse \(D\) und \(E\) stochastisch unabhängig sind.

   \(\mathbf{\color{green}{D}}\)   ‘’Die Summe der erzielten Zahlen ist kleiner als 4.‘’

   \(\mathbf{\color{green}{E}}\)   ‘’Das Produkt der erzielten Zahlen ist 2 oder 3.‘’

   (5 P)

Lösung

\(\\[2em]\)

Spiel mit dem Glücksrad

Jede spielende Person darf das Glücksrad beliebig oft drehen. Beendet sie das Spiel selbst, bevor sie eine \(0\) erzielt, so wird ihr die Summe der erzielten Zahlen in Euro ausgezahlt. Erzielt sie eine \(0\), so ist das Spiel dadurch beendet und es erfolgt keine Auszahlung.

\(\\\)

1. Eine erste Spielerin entscheidet sich vor dem Spiel dafür, das Glücksrad, sofern sie keine \(0\) erzielt, viermal zu drehen und danach das Spiel zu beenden.

   Bestimmen Sie die Wahrscheinlichkeit dafür, dass sie eine Auszahlung erhält.

   (2 P)

\(\\\)

2. Bei einer zweiten Spielerin beträgt nach mehrmaligen Drehen des Glücksrads die Summe der erzielten Zahlen 60. Die Spielerin entscheidet sich nun, das Glücksrad genau ein weiteres Mal zu drehen.

   Berechnen Sie in dieser Situation den Erwartungswert für die Auszahlung.

   (3 P)

\(\\\)

3. Wenn sich eine spielende Person vor dem Spiel dafür entscheidet, das Glücksrad, sofern sie keine \(0\) erzielt, \(n\)-mal zu drehen, dann kann der Erwartungswert für die Auszahlung mit dem Term

   \( \quad 5 \cdot n \cdot 0{,}9^n \)

   berechnet werden. Beurteilen Sie dazu folgende Aussage:

   ,,Es gibt zwei aufeinanderfolgende aber nicht drei aufeinanderfolgende Werte von n, für die die Erwartungswerte für die Auszahlung übereinstimmen.‘’

   (4 P)

Lösung

\(\\[2em]\)

Zehnseitiger Spielwürfel

Der Schüler Oskar legt einen zehnseitigen Spielwürfel mit dem Ziffern \(0\) bis \(9\) auf den Tisch und behauptet, dass alle Zahlen des Würfels wie beim Glücksrad mit der gleichen Wahrscheinlichkeit auftreten. Die Schülerin Ronja würfelt mehrfach damit und vermutet, dass die Zahl \(8\) mit einer geringeren Wahrscheinlichkeit als von Oskar behauptet, auftritt. Ronja plant einen Hypothesentest, um ihre Vermutung zu stützen.

1. Zunächst ermittelt Ronja die größte Anzahl \(k\), mit der die Zahl \(8\) bei \(240\) Durchführungen auftreten darf, damit ihre Vermutung auf einem Signifikanzniveau von \(3 \%\) noch gestützt wird.

   • Geben Sie die zugehörige Nullhypothese an und entscheiden Sie, ob ein rechtsseitiger oder ein linksseitiger Hypothesentest vorliegt.

   • Ermitteln Sie die Anzahl \(k\).

     (6 P)

\(\\\)

2. Schließlich hat Ronja, um die Vermutung zu stützen, einen einseitigen Hypothesentest mit einem Stichprobenumfang von \(n=175\) und einem Signifikanzniveau von \(r \%\)% erstellt. Dabei hat sie den Verwerfungsbereich

   \( \quad V = \{0; 1; 2; \dots ; 10 \} \)

   erhalten.

   Bestimmen Sie alle ganzen Zahlen, die Ronja für \(r\) gewählt haben könnte, die zu dem ermittelten Verwerfungsbereich passen.

   (4 P)

Lösung

\(\\[2em]\)

Spielfigur und Koordinatensystem

Ronja und Oskar haben ein Koordinatensystem gezeichnet und auf den Ursprung \((0|0)\) eine Spielfigur gestellt. Sie vereinbaren nun folgendes Spiel.

Das Glücksrad wird immer wieder gedreht. Tritt eine \(7\), eine \(8\) oder eine \(9\) auf, so darf Oskar die Spielfigur um zwei Einheiten nach oben (in \(y\)-Richtung) bewegen.
Tritt eine der anderen Zahlen auf, darf Ronja die Figur nur um eine Einheit nach rechts (in \(x\)-Richtung) verschieben.
Das Spiel endet mit einem Sieg für Ronja, wenn die Figur die \(x\)-Koordinate \(6\) erreicht hat. Oskar gewinnt, wenn die Figur die \(y\)-Koordinate \(6\) erreicht hat.

\(\\\)

1. Erläutern Sie, warum die Figur bei diesem Spiel den Punkt \((6|6)\) nicht erreichen kann.

   (2 P)

\(\\\)

2. Geben Sie an, wie oft Ronja und wie oft Oskar die Figur seit Spielbeginn bewegt haben, falls die Figur auf dem Punkt \(P(2|2)\) steht.

   Berechnen Sie, wie groß zu Spielbeginn die Wahrscheinlichkeit dafür ist, dass die Figur auf dem Punkt \(P\) zum Stehen kommt.

   (3 P)

\(\\\)

3. Bestimmen Sie, wie groß zu Spielbeginn die Wahrscheinlichkeit dafür ist, dass Ronja gewinnt.

   (6 P)

Lösung

\(\\[1em]\)