HMF 2 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Grad mindestens 3
\(f'(x_2) = 0\) und \(f''(x_2) \not= 0\) beschreibt einen Extrempunkt. Ein (lokales) Minimum der Ableitungsfunktion \(f'\) bedeutet einen Wendepunkt an der Stelle \(x_3\).
Eine ganzrationale Funktion mit (mindestens) einen Wendepunkt muss mindestens von Grad 3 sein.
\(\\[1em]\)
Aufgabe 2 – Skizze
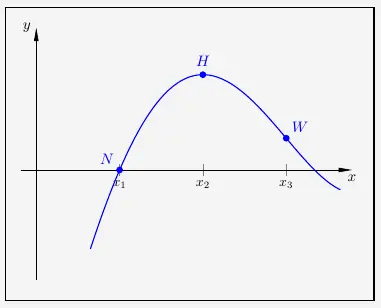
\(\\[1em]\)