Glücksrad drehen
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Zwanzigmal drehen
Das Drehen des Glücksrads ist binomialverteilt mit \(n=20\). Für eine ungerade Zahl ist die Wahrscheinlichkeit \(p=0{,}5\).
Die Wahrscheinlichkeit für Einzelwerte der Binomialverteilung wird berechnet mit der Bernoullikette
\( \quad P( = k) = \begin{smallmatrix} \left( \begin{array}{c} n \\ i \end{array} \right) \end{smallmatrix} p^i \cdot (1-p)^{n-i} \)
\(\\\)
und die der kumulierten (aufsummierten) Binomialverteilung mit
\( \quad P(x\leq k) = \displaystyle{\sum\limits_{i=1}^k} \begin{smallmatrix} \left( \begin{array}{c} n \\ i \end{array} \right) \end{smallmatrix} p^i \cdot (1-p)^{n-i} \)
\(\\\)
-
\(\text{Ereignis} \; \mathbf{\color{green}{A}}\)
Es gilt \(k=7\) und stellt sich graphisch wir folgt dar.
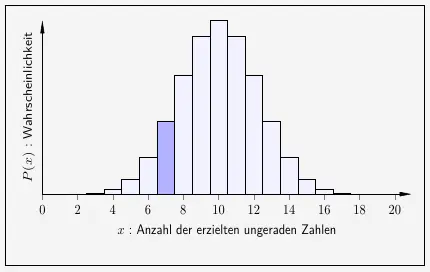
Die Wahrscheinlichkeit wird mit der Bernoulli-Formel berechnet, in der die Werte eingesetzt werden:
\( \quad P(x = 7) = \begin{smallmatrix} \left( \begin{array}{c} 20 \\ 7 \end{array} \right) \end{smallmatrix} \cdot 0{,}5^7 \cdot (1-0{,}5)^{20-7} \)
Alternativ kann dies mit der Dichtefunktion \(B_{ n ; p }(k)\) in der Tabelle für Binomialverteilungen abgelesen oder mit der entsprechenden Taschenrechnerfunktion berechnet werden.
\( \quad B_{ 20 \, ; \, 0{,}5 }(7) = 0{,}0739 = 7{,}39\% \)
\(\\\)
-
\(\text{Ereignis} \; \mathbf{\color{green}{B}}\)
Hier ist \(k < 9\). Die Wahrscheinlichkeit wird mit der kumulierten Binomialverteilung berechnet. Dabei gilt
\( \quad P(x < 9) = P(x \leq 8) \)

Es folgt die Berechnung mit
\( \quad P(x \leq 8) = \displaystyle{\sum\limits_{i=0}^8} \begin{smallmatrix} \left( \begin{array}{c} 20 \\ i \end{array} \right) \end{smallmatrix} \cdot 0{,}5^i \cdot (1-0{,}5)^{20-i} \)
oder vereinfacht mit Tabelle bzw. Taschenrechnerfunktion
\( \quad F_{ 20 \, ; \, 0{,}5 }(8) = 0{,}2517 = 25{,}17\% \)
\(\\\)
-
\(\text{Ereignis} \; \mathbf{\color{green}{C}}\)
Nun ist \(7 < k \leq 12\). Es gilt
\( \quad P(7 < x \leq 12) = P(x \leq 12) - P(x \leq 7) \)

Es folgt die Berechnung mit
\( \quad P(8 \leq x \leq 12) = \displaystyle{\sum\limits_{i=8}^12} \begin{smallmatrix} \left( \begin{array}{c} 20 \\ i \end{array} \right) \end{smallmatrix} \cdot 0{,}5^i \cdot (1-0{,}5)^{20-i} \)
oder mit Tabelle/Taschenrechnerfunktion
\( \quad F_{ 20 \, ; \, 0{,}5 }(12) - F_{ 20 \, ; \, 0{,}5 }(7) = 0{,}8684 - 0{,}1316 = 0{,}7368 = 73{,}68\% \)
\(\\[2em]\)
Aufgabe 2 – Zweimal drehen
Das Ereignis \(D\) ist
\( \quad D = \{ (0,0) \, ; \; (0,1) \, ; \; (0,2) \, ; \; (0,3) \, ; \; (1,0) \, ; \; (1,1) \, ; \; (1,2) \, ; \; (2,0) \, ; \; (2,1) \, ; \; (3,0) \} \)
\(\\\)
und enthält \(10\) Elemente.
Das Ereignis \(E\) ist
\( \quad E = \{ (1,2) \, ; \; (2,1) \, ; \; (1,3) \, ; \; (3,1) \} \)
\(\\\)
und enthält \(4\) Elemente.
Das Ereignis \(D \cap E\) ist
\( \quad D \cap E = \{ (1,2) \, ; \; (2,1) \} \)
\(\\\)
mit \(2\) Elemente.
Insgesamt gibt es beim zweimaligen Drehen \(100\) Elemente mit
\( \quad \Omega = \{ (0,0) \, ; \; \; \cdots \; \; ; \, (9,9) \} \)
\(\\\)
Daraus ergibt sich die Vierfeldertafel mit den absoluten Häufigkeiten.
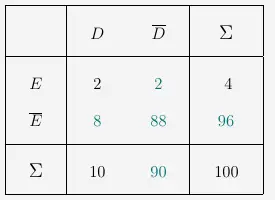
\(\\\)
woraus die Vierfeldertafel mit den relativen Häufigkeiten entsteht.

\(\\\)
Für die stochastische Unabhängigkeit gilt
\( \quad P(A) \cdot P(B) \, = \, P( A \cap B ) \)
\(\\\)
Wir untersuchen dies für das Ereignis \(D\) und \(E\).
\( \quad P(D) \cdot P(E) \, = \, 0{,}04 \cdot 0{,}1 \, = \, 0{,}004 \, \not= \, 0{,}02 \, = \, P( D \cap E ) \)
\(\\\)
Damit sind die Ereignisse \(D\) und \(E\) nicht stochastisch unabhängig.
\(\\[1em]\)