Funktionenschar
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Skizze
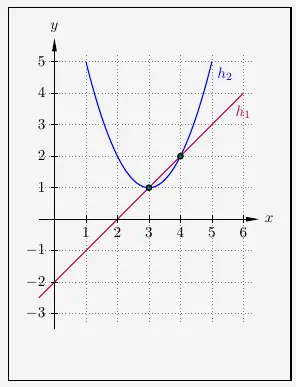
\(\\[2em]\)
Aufgabe 2 – Linksseitiges Randverhalten
Gerade Werte von \(k\) :
\( \quad \lim \limits_{x \to -\infty} h_k(x) \; = \; \infty \)
\(\\\)
Ungerade Werte von \(k\) :
\( \quad \lim \limits_{x \to -\infty} h_k(x) \; = \; -\infty \)
\(\\[2em]\)
Aufgabe 3 – Schnittpunkte
Punkte, die alle Graphen gemeinsam haben, sind die Schnittpunkte aller Graphen. Damit die Schnittpunktberechnung allgemeingültig für alle Graphen der Schar ist, definieren wir nun Folgendes:
\( \quad a \in k \; , \quad b \in k \quad \text{und} \quad a < b \)
\(\\\)
Es existieren
\( \quad h_a(x) = (x - 3)^a + 1 \quad \text{und} \quad a \in \mathbb{N}\setminus \{0\} \)
\(\\\)
und
\( \quad h_b(x) = (x - 3)^b + 1 \quad \text{und} \quad b \in \mathbb{N}\setminus \{0\} ,0\} \)
\(\\\)
wobei \(h_a\) und \(h_b\) voneinander verschieden sind. Wir berechnen deren Schnittpunkte mit
\( \quad \begin{array}{ r c l l } h_b(x) & = & h_a(x) & \\[6pt] (x - 3)^b + 1 & = & (x - 3)^a + 1 & | \, -1 \\[6pt] (x - 3)^b & = & (x - 3)^a & | \, : \left( (x - 3)^a \right) \\[6pt] \frac{(x - 3)^b}{(x - 3)^a} & = & 1 & \\[6pt] (x - 3)^{\frac{b}{a}} & = & 1 & \\ \end{array} \)
\(\\\)
Da nun
\( \quad 1^n \, = \, \underbrace{1 \cdot 1 \cdot 1 \cdot 1 \dots 1}_{n-mal} \, = \, 1 \)
\(\\\)
ist, gilt auch
\( \quad \begin{array}{ r c l } 1^{\frac{b}{a}} & = & 1 \\[8pt] (4 - 3)^{\frac{b}{a}} & = & 1 \\ \end{array} \)
\(\\\)
Damit folgt \(x_1 = 4\).
\(\\\)
Die zweite Lösung erhalten wir schon einen Schritt früher mit
\( \quad \begin{array}{ r c l } (x - 3)^b & = & (x - 3)^a \\ \end{array} \)
\(\\\)
Es gilt nun
\( \quad 0 \, = \, 0 \quad \Leftrightarrow \quad 0^b \; = \, 0^a \)
\(\\\)
Dementsprechend muss
\( \quad \begin{array}{ r c l l } x - 3 & = & 0 & | \, +3 \\[5pt] x_2 & = & 3 \\ \end{array} \)
\(\\\)
sein.
\(\\[2em]\)
Aufgabe 4 – Nullstellen
Es gilt
\( \quad \begin{array}{ r c l l } h_k(x) & = & 0 \\[12pt] (x-3)^k + 1 & = & 0 & | \, -1 \\[5pt] (x-3)^k & = & -1 & | \, \sqrt[k]{\dots} \\[5pt] \end{array} \)
\(\\\)
Aus negativen Zahlen können nur Wurzeln mit ungeraden \(k\) gezogen werden. Folglich gibt es für gerade \(k\) keine Lösung.
\( \quad \begin{array}{ r c l l } (x-3)^k & = & -1 & | \, \sqrt[k]{\dots} \\[5pt] x -3 & = & -1 & | \, +3 \\[5pt] x & = & 2 \\ \end{array} \)
\(\\\)
Nur für ungerade \(k\) existiert eine Lösung mit \(N(2|0)\).
\(\\[2em]\)
Aufgabe 5 – Trapez
Das Viereck ist ein Trapez
Da Punkt \(R\) und \(S\) den \(x\)-Wert \(x=2\) haben und \(P\) und \(Q\) den \(x\)-Wert \(x=4\) haben, ergibt sich ein Viereck mit zwei vertikalen Kanten. Laut Definition ist ein Trapez ein ebenes Viereck mit zwei parallelen Seiten. Das ist hier gegeben.
Mögliche Vierecke, die jetzt noch entstehen könnten, wären ein Parallelogramm, eine Raute, ein Rechteck oder ein Quadrat. Dies sind jedoch Sonderformen des Trapezes. Damit muss sich ein Trapez durch die Punkte \(R\),\(S\), \(P\) und \(Q\) ergeben.
\(\\[1em]\)
Flächeninhalt von 2k
Die Fläche eines Trapezes
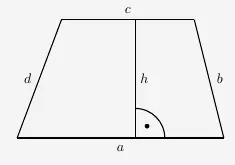
\(\\\)
wird berechnet mit
\( \quad A \; = \; \frac{a + c}{2} \cdot h \)
\(\\\)
Die Höhe \(h\) ist in diesem Fall der Abstand der Strecken \(\overline{RS}\) und \(\overline{PQ}\), also \(2\) LE.
Die Strecken \(a=\overline{RS}\) und \(c=\overline{PQ}\) werden berechnet mit
\( \quad \begin{array}{ r c l } \overline{RS} & = & \bigl| h_k(2) - h_k'(2) \bigr| \\[6pt] \overline{RS} & = & \sqrt{ \left(h_k(2) - h_k'(2) \right)^2 } \\ \end{array} \)
\(\\\)
und
\( \quad \begin{array}{ r c l } \overline{QP} & = & \bigl| h_k'(4) - h_k(4) \bigr| \\[6pt] \overline{QP} & = & \sqrt{ \left(h_k'(4) - h_k(4) \right)^2 } \\ \end{array} \)
\(\\\)
Wir benötigen die Ableitung von \(h_k\). Mit der Kettenregel ergibt sich
\( \quad \begin{array}{ r c l } h_k'(x) & = & k \cdot (x - 3)^{k-1} \\[6pt] & = & k \cdot \frac{(x - 3)^k}{x - 3} \\ \end{array} \)
\(\\\)
Daraus folgt
\( \quad \begin{array}{ r c l } \overline{RS} & = & \sqrt{ \left(h_k(2) - h_k'(2) \right)^2 } \\[10pt] & = & \sqrt{ \left((2 - 3)^k - k \cdot \frac{(2 - 3)^k}{2 - 3}\right)^2} \\[12pt] & = & \sqrt{ \left((-1)^k - k \cdot \frac{(-1)^k}{-1}\right)^2} \\[12pt] & = & \sqrt{ \left((-1)^k + k \cdot (-1)^k\right)^2} \\[12pt] & = & \sqrt{ \big((1 + k) \cdot(-1)^k\big)^2} \\[12pt] & = & \sqrt{ (1 + k)^2 \cdot(-1)^{2k}} \\[12pt] & = & \sqrt{ (1 + k)^2 \cdot 1} \\[12pt] & = & \sqrt{ (1 + k)^2} \\[12pt] & = & 1 + k \\ \end{array} \)
\(\\\)
und
\( \quad \begin{array}{ r c l } \overline{QP} & = & \sqrt{ \left(h_k'(4) - h_k(4) \right)^2 } \\[10pt] & = & \sqrt{ \left(k \cdot \frac{(4 - 3)^k}{4 - 3} - (4 - 3)^k\right)^2} \\[12pt] & = & \sqrt{ \left( k \cdot \frac{1^k}{1} - 1^k\right)^2} \\[12pt] & = & \sqrt{ \left( k \cdot \frac{1}{1} - 1\right)^2} \\[12pt] & = & \sqrt{( k - 1)^2} \\[12pt] & = & k - 1 \\ \end{array} \)
\(\\\)
Eingesetzt in die Flächenformel des Trapezes ist
\( \quad \begin{array}{ r c l } A & = & \frac{\overline{RS} + \overline{PQ}}{2} \cdot 2 \\[6pt] & = & \overline{RS} + \overline{PQ} \\[6pt] & = & 1 + k + k - 1 \\[6pt] & = & 2 k \\ \end{array} \)
\(\\[1em]\)