Ebene N
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Schnittfläche
Mit der Gleichung von der Ebene \(N_k\)
\( \quad \begin{array}{ r c l l } -3x_1 + 6x_2 & = & 0 & | \, +3x_1 \\[6pt] 6x_2 & = & 3x_1 & | \, : 3 \\[6pt] 2x_2 & = & x_1 \\ \end{array} \)
\(\\\)
folgt, dass die \(x_1\)-Werte doppelt so groß sind wie die \(x_2\)-Werte. Das heißt dass in der \(x_1x_2\)-Ebene der Ursprung \(O(0|0|0)\) und der Punkt \(A(6|3|0)\) und alle Punkte auf der Verbindung der beiden zu der Ebene \(N_k\) gehören.
Daraus ergibt sich die farbig dargestellte Schnittfläche des Körpers.
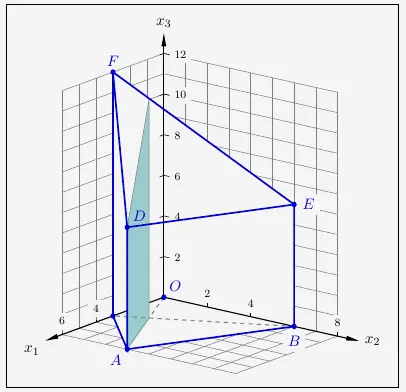
\(\\[2em]\)
Aufgabe 2 – Geschnittene Kanten
Für \(k=0\) erhalten wir den Punkt \(P_0(1|0|0)\) und für \(k=1\) erhalten wir den Punkt \(P_1(0|1|0)\). Alle anderen Punkte \(P_k\) liegen zwischen diesen beiden Punkten. Damit liegt \(P_k\) immer in der \(x_1x_2\)-Ebene. Da die \(x_3\)-Achse ebenfalls zur Ebene \(N_k\) gehört, muss \(N_k\) orthogonal zur \(x_1x_2\)-Ebene sein.
Insgesamt stellt \(N_k\) die Schar der Ebenen dar, die zwischen der \(x_1\)-Achse und der \(x_2\)-Achse senkrecht auf der \(x_1x_2\)-Ebene stehen einschließlich der Ebenen auf diesen Achsen. Alle diese Ebenen enthalten den Koordinatenursprung \(O(0|0|0)\) als Punkt.
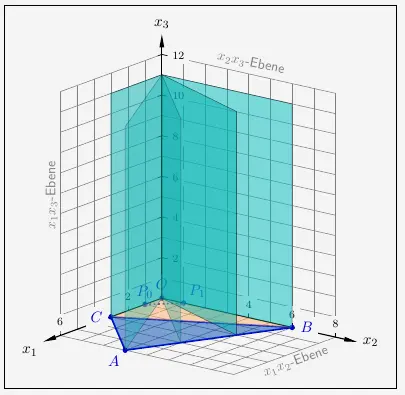
Jede dieser Ebenen schneidet die Kante \(\overline{BC}\). Im Gegensatz dazu wird die Kante \(\overline{CA}\) nur von einem Teil der Ebenen geschnitten. Der andere Teil schneidet die Kante \(\overline{AB}\).
Welches nun den größeren Bereich ausmacht können wir bestimmen, indem wir die \(k\)-Werte dieser Bereiche ermitteln.
Dazu gehen wir folgendermaßen vor:
Zunächst wird die Gerade durch die Punkte \(P_0\) und \(P_1\) sowie die Gerade durch die Punkte \(O\) und \(A\) aufgestellt. Der Schnittpunkt liefert Aussagen über \(k\), so dass die Bereiche links und rechts der Ebene, die den Punkt \(A\) enthält, beurteilt werden können.
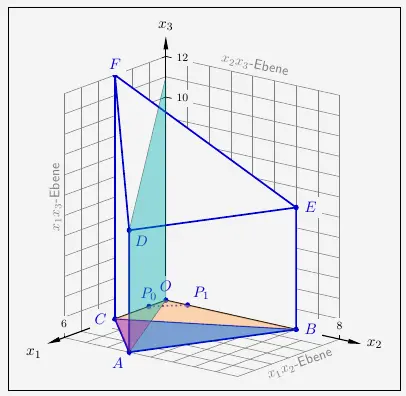
\( \quad \begin{array}{ r c c c l } g_{OA}: \; \overrightarrow{x} & = & r \cdot \overrightarrow{OA} & = & r \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
\( \quad \begin{array}{ r c l } g_{P_0P_1}: \; \overrightarrow{x} & = & \overrightarrow{P_0} + s \cdot \overrightarrow{P_ 1P_2} \\[6pt] & = & \overrightarrow{P_0} + s \cdot \left( \overrightarrow{P_2} - \overrightarrow{P_1} \right) \\[6pt] & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{1} \\ \scriptstyle{0} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} + s \cdot \left[ \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{0} \\ \scriptstyle{1} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{1} \\ \scriptstyle{0} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} \right] \\[8pt] & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{1} \\ \scriptstyle{0} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{-1} \\ \scriptstyle{1} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix}\\ \end{array} \)
\(\\\)
Zur Schnittpunktberechnung werden die beiden Geraden gleichgesetzt.
\( \quad \begin{array}{ r c c c l } r \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{1} \\ \scriptstyle{0} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{-1} \\ \scriptstyle{1} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix}\\ \end{array} \)
\(\\\)
\( \quad \begin{array}{ l } \left. \begin{array}{ c r*{8}{r} l } \textrm{I} && 6r & = & 1 & - & s && \\[3pt] \textrm{II} && 3r & = & & & s && \\ \end{array} \quad \right]_{\Rightarrow \; \textrm{(II a)}}^+ \begin{array}{ l } \\[24pt] \end{array} \\ \begin{array}{ c*{9}{c} l } \textrm{III} && 0 & = & 0 && \\ \end{array} \end{array} \)
\(\\\)
\( \quad \begin{array}{ c r*{4}{r} l } \textrm{II a)} & 9r & = & 1 & | \, :9 \\[5pt] & r & = & \frac{1}{9} & \\ \end{array} \)
\(\\\)
\(r\) in \(\textrm{II}\) :
\( \quad \begin{array}{ r c l } 3 \cdot \frac{1}{9} & = & s \\[5pt] \frac{1}{3} & = & s \\ \end{array} \)
\(\\\)
Es existiert genau eine Lösung mit \(r = \frac{1}{9}\) und \(s = \frac{1}{3}\).
\(\\\)
\(r\) in \(g_{OA}\) eingesetzt ergibt
\( \quad \begin{array}{ r c c c l } \overrightarrow{x} & = & \frac{1}{9} \cdot \begin{smallmatrix} \left( \begin{array}{r} \scriptstyle{6} \\ \scriptstyle{3} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} \scriptstyle{\frac{2}{3}} \\ \scriptstyle{\frac{1}{3}} \\ \scriptstyle{0} \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\\)
Nach der Festlegung für \(P_k\) ist
\( \quad x_2 \; = \; \frac{1}{3} \; = \; k \)
\(\\\)
Daraus folgt, dass die Kante \(\overline{CA}\) geschnitten wird für \(k \in \left] 0 ; \frac{1}{3} \right[\) und die Kante \(\overline{AB}\) für \(k \in \left] \frac{1}{3} ; 1 \right[\).
Der zweite Bereich ist der Größere. Es werden also dort die Kanten \(\overline{CB}\), \(\overline{AB}\) und auch die darüberliegende Kante \(\overline{DE}\) geschnitten. Ferner wird noch und die schräg nach oben und leicht nach vorne verlaufende Kante \(\overline{EF}\) geschnitten.
\(\\[1em]\)