Zehnseitiger Würfel
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Signifikanztest
Der Versuch mit dem zehnseitigen Würfel ist binomialverteilt mit dem Ereignis eine \(8\) zu würfeln. Dabei ist \(n=240\).
Vermutung:
,,Die Wahrscheinlichkeit eine \(8\) zu würfeln beträgt weniger als 10%.‘’
\(\\\)
Die Vermutung ist nachzuweisen. Mit dem Wissen, dass jede Zahl mit der Wahrscheinlichkeit von \(10\%\) fällt, legen wir die Nullhypothese damit fest. Die \(h_1\)-Hypothese ist die Gegenhypothese.
-
\(h_1: \; p < 0{,}1\)
-
\(h_0: \; p = 0{,}1\)
Die Nullhypothese ist unsere Arbeitshypothese.
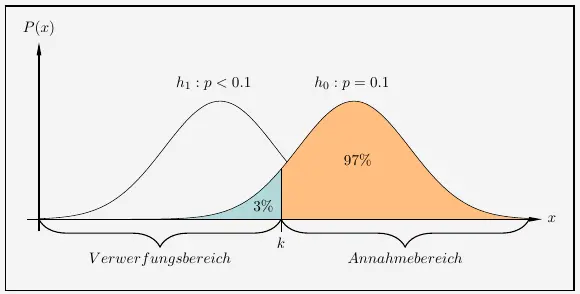
Wir grenzen die Nullhypothese nach links gegen die \(h_1\)-Hypothese ab. Dann untersuchen wir den linksseitigen Verwerfungsbereich der Nullhypothese, der das Signifikanzniveau enthält. Folglich muss es sich hier um einen linksseitigen Signifikanztest handeln.
\(\\[1em]\)
Anzahl k bestimmen
Mit dem Signifikanzniveau \(\alpha = 3\%\) im Verwerfungsbereich von \(h_0\) gilt
\( \quad P(x \leq k) \, \leq \, 0{,}03 \)
\(\\\)
Mit dem Taschenrechner können wir mit der inversen Normalenverteilung näherungsweise den Wert für\(k\) ermitteln.
Wir benötigen dazu den Erwartungswert mit
\( \quad \mu \, = \, n \cdot p \, = \, 240 \cdot 0{,}1 \, = \, 24 \)
\(\\\)
und die Standardabweichung mit
\( \quad \sigma \, = \, \sqrt{n \cdot p \cdot (1-p)} \, = \, \sqrt{240 \cdot 0{,}1 \cdot 0{,}9} \, = \, \sqrt{21{,}6} \, \approx \, 4{,}65 \)
\(\\\)
Mit den Taschenrechnerfunktionen geben wir bei der inversen Normalverteilung die Werte
\( \quad \begin{array}{ r c l } \text{Fläche} & = & 0{,}03 \\[5pt] \sigma & = & \sqrt{21{,}6} \\[5pt] \mu & = & 24 \\ \end{array} \)
\(\\\)
ein und erhalten
\( \quad \begin{array}{ r c l c l } k & = & 15{,}26 & \approx & 15\\ \end{array} \)
\(\\\)
Zur Kontrolle kann mit der kumulierten Binomialverteilung das Ergebnis überprüft werden.
\( \quad \begin{array}{ | c | c | } \hline \mathbf{k} & \mathbf{P(x \leq k)} \\ \hline 13 & 0{,}0080 \\ 14 & 0{,}0154 \\ 15 & 0{,}0279 \\ 16 & 0{,}0475 \\ \hline \end{array} \)
\(\\\)
Auch hier zeigt sich, dass \(k=15\) der richtige Wert ist.
\(\\[2em]\)
Aufgabe 2 – Zahl r des Verwerfungsbereiches
Mit dem Verwerfungsbereich lässt sich mit der kumulierten Binomialverteilung der Wert \(r\) ermitteln.
\( \quad r \, = \, P(x \leq 10) \, = \, 0{,}0318 \)

\(\\\)
Offensichtlich ist das Signifikanzniveau mit \(r=3\) zu klein. Denn dort hätten wir nur den Verwerfungsbereich \([0;9]\). Folglich gilt für \(r\), der ja nur ganzzahlige Werte haben darf, mindestens \(r=4\).
Um weitere Werte zu bestimmen, berechnen wir
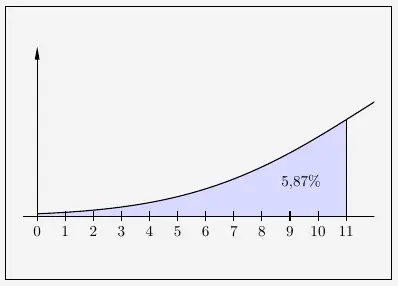
\( \quad r \, = \, P(x \leq 11) \, = \, 0{,}0587 \)
\(\\\)
Wie hier zusehen ist, beinhaltet \(r=5\) auch den Verwerfungsbereich \([0;10]\). Denn der Verwerfungsbereich \([0;11]\) beginnt ja erst ab \(r=5{,}87\).
Damit gelten die ganzzahligen Werte \(r=4\) und \(r=5\).
\(\\[1em]\)