HMF 8 - Lösung
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Mittelsenkrechte
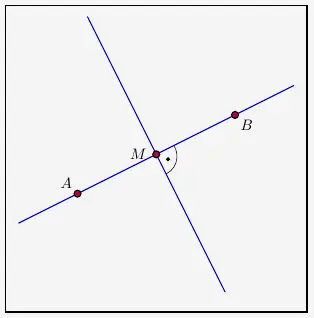
Damit \(g\) eine Mittelsenkrechte ist, muss der Stützvektor der Geraden \(g\) den Mittelpunkt \(M\) zwischen \(A\) und \(B\) ausdrücken. Wir überprüfen dies mit
\( \quad \begin{array}{ r c l } \overrightarrow{a} + \frac{1}{2} \cdot \overrightarrow{AB} & = & \overrightarrow{a} + \frac{1}{2} \cdot \left(\overrightarrow{b} - \overrightarrow{a}\right) \\[6pt] & = & \begin{smallmatrix} \left( \begin{array}{r} 7 \\ 3 \\ 1 \end{array} \right) \end{smallmatrix} + \dfrac{1}{2} \cdot \left[ \begin{smallmatrix} \left( \begin{array}{r} 1 \\ -3 \\ 1 \end{array} \right) - \left( \begin{array}{r} 7 \\ 3 \\ 1 \end{array} \right) \end{smallmatrix} \right] \\[8pt] & = & \begin{smallmatrix} \left( \begin{array}{r} 7 \\ 3 \\ 1 \end{array} \right) \end{smallmatrix} + \dfrac{1}{2} \cdot \begin{smallmatrix} \left( \begin{array}{r} -6 \\ -6 \\ 0 \end{array} \right) \end{smallmatrix} \\[8pt] & = & \begin{smallmatrix} \left( \begin{array}{r} 7 \\ 3 \\ 1 \end{array} \right) \end{smallmatrix} + \begin{smallmatrix} \left( \begin{array}{r} -3 \\ -3 \\ 0 \end{array} \right) \end{smallmatrix} \\[8pt] & = & \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 0 \\ 1 \end{array} \right) \end{smallmatrix} \\[6pt] & = & \, \overrightarrow{m} \end{array} \)
\(\\\)
Nun ist noch zu überprüfen, ob \(g\) senkrecht auf der Strecke \(\overline{AB}\) steht. Wir verwenden den Richtungsvektor von \(g\) und den Vektor \(\overrightarrow{AB}\).
\( \quad \begin{smallmatrix} \left( \begin{array}{r} 2 \\ -2 \\ 1 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{r} -6 \\ -6 \\ 0 \end{array} \right) \end{smallmatrix} =2 \cdot(-6) - 2 \cdot (-6) + 1 \cdot 0 = 0 \)
\(\\\)
Damit ist \(g\) die Mittelsenkrechte der Strecke \(\overline{AB}\).
\(\\[2em]\)
Aufgabe 2 – Dreiecke
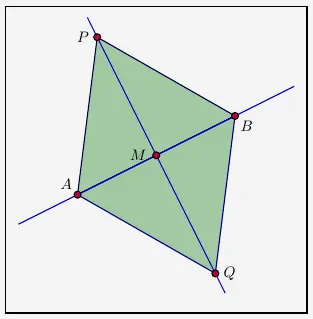
Die Fläche eines Dreiecks wird berechnet mit
\( \quad A = \frac{g \cdot h}{2} \)
\(\\\)
Mit
\( \quad \begin{array}{ l } g \; = \; \overline{AB} \; = \; \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} -6 \\ -6 \\ 0 \end{array} \right) \end{smallmatrix} \end{vmatrix} \; = \; \sqrt{(-6)^2 + (-6)^2} \; = \; 6 \sqrt{2} \end{array} \)
\(\\\)
ergibt sich die Länge \(h = \overline{MP}\) durch
\( \quad \begin{array}{ r c l l } A & = & \frac{\overline{AB} \cdot h}{2} \\[6pt] 9 \sqrt{2} & = & \frac{6\sqrt{2} \cdot h}{2} & \bigl| \, \cdot 2 \\[6pt] 18 \sqrt{2} & = & 6\sqrt{2} \cdot h & \bigl| \, : (6\sqrt{2}) \\[6pt] 3 & = & h \\ \end{array} \)
\(\\\)
Punkt \(P\) und \(Q\) befinden sich also \(3\) Einheiten auf der Gerade \(g\) liegend von Punkt \(M\) entfernt. Wir benötigen nun die Länge des Richtungsvektors von \(g\).
\( \quad \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} 2 \\ -2 \\ 1 \end{array} \right) \end{smallmatrix} \end{vmatrix} = \sqrt{2^2 + (-2)^2 + 1^2} = \sqrt{9} = 3 \)
\(\\\)
Punkt \(P\) kann also einfach berechnet werden mit
\( \quad \begin{array}{ r c l } \overrightarrow{p} & = & \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 0 \\ 1 \end{array} \right) \end{smallmatrix} + \begin{smallmatrix} \left( \begin{array}{r} 2 \\ -2 \\ 1 \end{array} \right) \end{smallmatrix} = \begin{smallmatrix} \left( \begin{array}{r} 6 \\ -2 \\ 2 \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\\)
und Punkt \(Q\) mit
\( \quad \begin{array}{ r c l } \overrightarrow{q} & = & \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 0 \\ 1 \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} 2 \\ -2 \\ 1 \end{array} \right) \end{smallmatrix} = \begin{smallmatrix} \left( \begin{array}{r} 2 \\ 2 \\ 0 \end{array} \right) \end{smallmatrix} \end{array} \)
\(\\\)
Wir erhalten damit die Punkte
\( \quad P\left(6 \, | -2 \, | \, 2\right) \quad \text{und} \quad Q\left(2 \, | \, 2 \, | \, 0\right) \)
\(\\\)
oder alternativ
\( \quad P\left(2 \, | \, 2 \, | \, 0\right) \quad \text{und} \quad Q\left(6 \, | -2 \, | \, 2\right). \)
\(\\[1em]\)