Spurpunkte und Projektionen
Inhaltsverzeichnis
\(\\\)
Bei Spurpunkten und Projektionen geht es um die Schnittpunkte mit den Koordinatenachsen und den Koordinatenebenen.
Während sich die Spurpunkte mit den Schnittpunkten der Koordinatenachsen beschäftigen, behandeln die Projektionen die Schnittpunkte mit den Koordinatenebenen.
\(\\[1em]\)
Koordinatenachsen und Koordinatenebenen
Koordinatenachsen können sowohl 2-dimensional
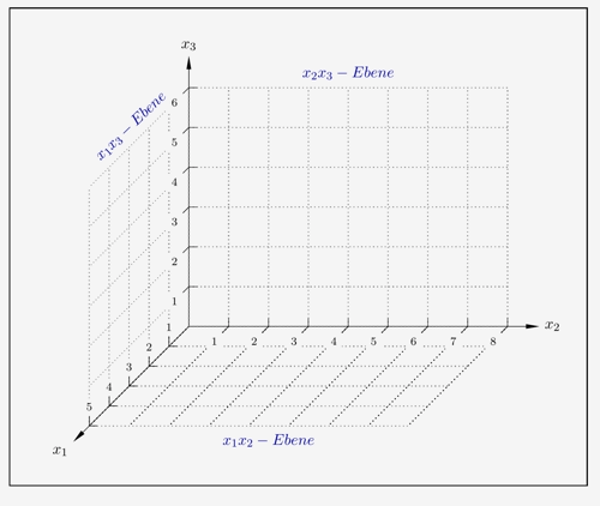
als auch 3-dimensional
vorkommen. Das hängt jeweils von der Art der verwendeten Vektoren ab.
Im 2-dimensionalen Koordinatensystem ist die waagerechte Achsen die \(x_1\)-Achse, auch als \(x\)-Achse bezeichnet, und die senkrechte Achse die \(x_2\)-Achse, auch als (y)-Achse bezeichnet; entsprechend der Notation in der Analysis.
\(\\\)
Im 3-dimensionalen Koordinatensystem ist die nach vorne verlaufende Achse die \(x_1\)-Achse und gegen den Uhrzeigersinn folgen die \(x_2\)-Achse und die \(x_3\)-Achse. Auf dem karierten Papier ist eine Einheit in \(x_2\)-Richtung und in \(x_3\)-Richtung 2 Kästchen und wegen der räumlichen Verkürzung in \(x_1\)-Richtung ein diagonales Kästchen.
Wie hier zu sehen ist, entstehen durch die 3 Achsen die Koordinatenebenen, die ihre Bezeichnung durch die Achsen erhalten, von den sie aufgespannt werden.
Auch im 3-dimensionalen Koordinatensystem können die Bezeichnungen
\(x\)-Achse für die \(x_1\)-Achse,
\(y\)-Achse für die \(x_2\)-Achse,
\(z\)-Achse für die \(x_3\)-Achse
verwendet werden.
\(\\[2em]\)
Spurpunkte
Spurpunkte im Regelfall
Liegt eine Ebene in der Koordinatenform in der Form
\( \quad E: \; ax_1 + bx_2 + cx_3 = d \)
\(\\\)
mit
\( \quad \begin{array}{l} a \not= 0 \, , \\[4pt] b \not= 0 \, , \\[4pt] c \not= 0 \\ \end{array} \)
\(\\\)
vor, wie zum Beispiel bei der Ebene
\( \quad E: \; 15x_1 + 12x_2 + 20x_3 = 60 \, , \)
\(\\\)
so ergeben sich Schnittpunkte mit allen 3 Achsen. Diese werden als die Spurpunkte \(S_1\), \(S_2\) und \(S_3\) bezeichnet.
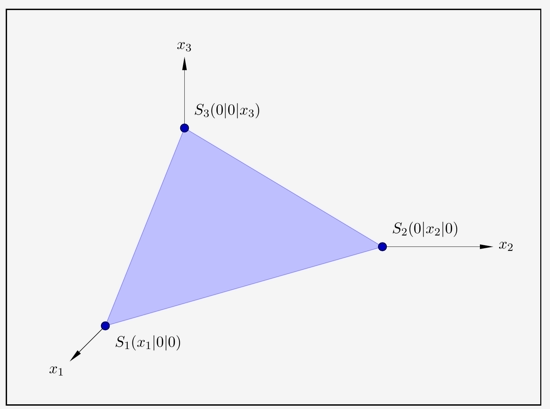
Die Spurpunkte werden nun folgendermaßen ermittelt:
Für \(S_1\) gilt, dass sowohl \(x_2=0\) als \(x_3=0\) sind. Dies in die Ebenengleichung eingesetzt ergibt
\( \quad \begin{array}{ r c l l } 15x_1 & = & 60 & | \, : 15 \\[4pt] x_1 & = & 4 & \\ \end{array} \)
\(\\\)
Es ergibt sich \(S_1(4|0|0)\).
\(\\\)
Entsprechend setzen wir für den Spurpunkte \(S_2\) die Werte \(x_1=x_3=0\) und für den Spurpunkte \(S_3\) die Werte \(x_1=x_2=0\).
Daraus ergeben sich die weiteren Spurpunkte \(S_2(0|5|0)\) und \(S_3(0|0|3)\).
\(\\[1em]\)
Sonderfall mit einem Spurpunkt
Liegt eine Ebene parallel zu einer Koordinatenebene, so ergibt sich genau 1 Spurpunkt.
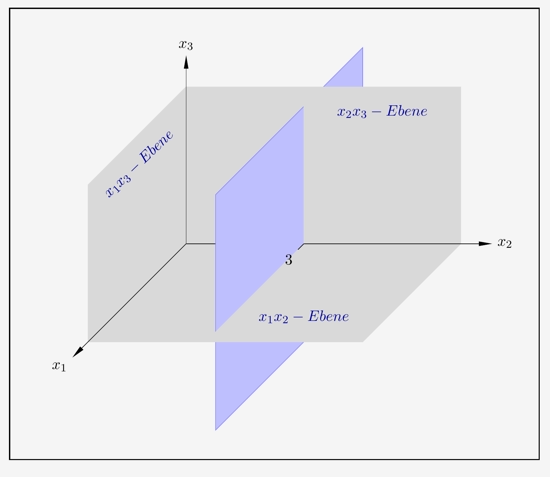
In diesem Fall liegt die Ebene parallel zur \(x_1x_3\)-Ebene mit dem Spurpunkt \(S_2(0|3|0)\). Die zugehörige Koordinatenform laut \(x_2=3\). Das bedeutet, dass alle Punkte der Ebene den \(x_2\)-Wert 3 haben.
\(\\[1em]\)
Sonderfall mit 2 Spurpunkten
Liegt eine Ebene parallel zu einer Koordinatenachse, so existieren nur 2 Spurpunkte der Ebene.
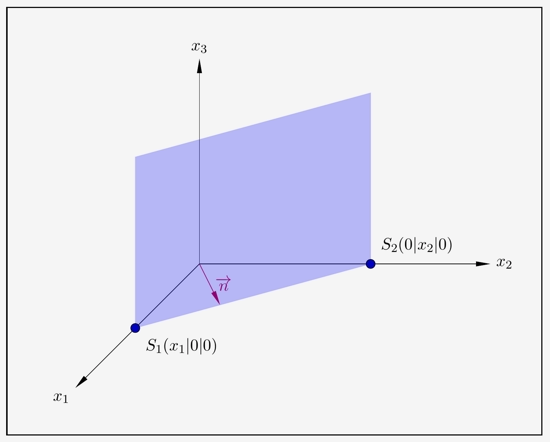
In diesem Fall liegt die Ebene parallel zur \(x_3\)-Achse. Das bedeutet, dass der Normalenvektor nur in \(x_1\)-Richtung und in \(x_2\)-Richtung verläuft. Es gibt also nur 2 Komponenten in der Koordinatenform der Ebene. Wir betrachten die Ebene
\( \quad E: \; 4x_1 + 3x_2 = 12 \)
\(\\\)
Für den Spurpunkt \(S_1\) wird \(x_2=0\) gesetzt und in die Gleichung eingefügt. Wir erhalten \(S_1(3|0|0)\). Entsprechend ergibt sich \(S_2(0|4|0)\).
\(\\[1em]\)
Spurgeraden
Eine Spurgerade verläuft jeweils durch 2 Spurpunkte. Als Beispiel verwenden wir die Ebene mit den 3 Spurpunkten und nehmen die Gerade durch \(S_1\) und \(S_2\).
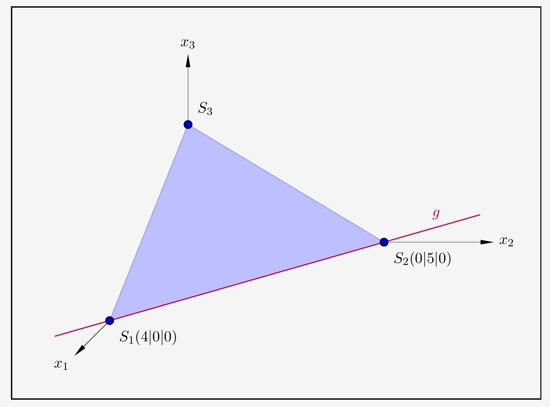
Es bieten sich hier also 2 mögliche Lösungsansätze an:
\(\\[1em]\)
Berechnung der Schnittgeraden von 2 Ebenen
Die \(x_1x_2\)-Ebene ist der ebene Boden des Koordinatensystems. Das heißt, dass \(x_3=0\) gilt. Eingesetzt in Ebene \(L\) erhalten wir
\( \quad \begin{array}{ r c l l } 15x_1 + 12x_2 + 20 \cdot 0 & = & 60 \\[4pt] 15x_1 + 12x_2 & = & 60 \\ \end{array} \)
\(\\\)
Weiter setzen wir \(x_1 = t\) und lösen nach \(x_2\) auf.
\( \quad \begin{array}{ r c l l } 15t + 12x_2 & = & 60 & | \, -15t \\[4pt] 12x_2 & = & 60 - 15t & | \, : 12 \\[5pt] x_2 & = & 5 - \frac{5}{4} t \\ \end{array} \)
\(\\\)
Mit den \(x\)-Werten
\( \quad \begin{array}{ r c l } x_1 & = & t \\[4pt] x_2 & = & 5 - \frac{5}{4} t \\[4pt] x_3 & = & 0 \\ \end{array} \)
\(\\\)
ergibt sich die Schnittgerade
\( \quad \begin{array}{ r c r c l } \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{r} x_1 \\ x_2 \\ x_3 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{ c c c } & & t \\ 5 & - & \frac{5}{4} t \\ 0 & & \end{array} \right) \end{smallmatrix} \\[6pt] & & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 0 \\ 5 \\ 0 \end{array} \right) \end{smallmatrix} + \begin{smallmatrix} \left( \begin{array}{r} t \\ -\frac{5}{4} t \\ 0 \end{array} \right) \end{smallmatrix}\\[6pt] & & g: \; \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 0 \\ 5 \\ 0 \end{array} \right) \end{smallmatrix} + \, t \, \cdot \begin{smallmatrix} \left( \begin{array}{r} 1 \\ -\frac{5}{4} \\ 0 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\[1em]\)
Aufstellen der Spurgeraden mit 2 Spurpunkten
In diesem Fall sind die Spurpunkte bereits bekannt aus der obigen Rechnung. Das vereinfacht wesentlich die Ermittlung der Spurgeraden \(g\) mit diesem Lösungsweg.
\( \quad \begin{array}{ l r c l } g: & \overrightarrow{x} & = & \overrightarrow{s_1} + t \cdot \overrightarrow{S_1S_2} \\[8pt] & \overrightarrow{x} & = & \overrightarrow{s_1} +t \cdot \Big(\overrightarrow{s_2} - \overrightarrow{s_2}\Big) \\[6pt] & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} + t \cdot \left[ \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 5 \\ 0 \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} \right] \\[6pt] & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{r} 4 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} -4 \\ 5 \\ 0 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\[2em]\)
Projektionen
Unter einer Projektion versteht man die Übertragung eines Objektes wie
- einem Punkt
- einer Strecke
- einer Fläche
- einem Körper
auf eine Koordinatenebene. Es können nun 5 Fälle unterschieden werden:
\(\\\)
Projektion orthogonal auf eine Koordinatenebene
Fällt paralleles Licht orthogonal auf eine Koordinatenebene, so wird ein Objekt, in diesem Fall ein Dreieck, als Schatten auf der jeweiligen Ebene dargestellt.
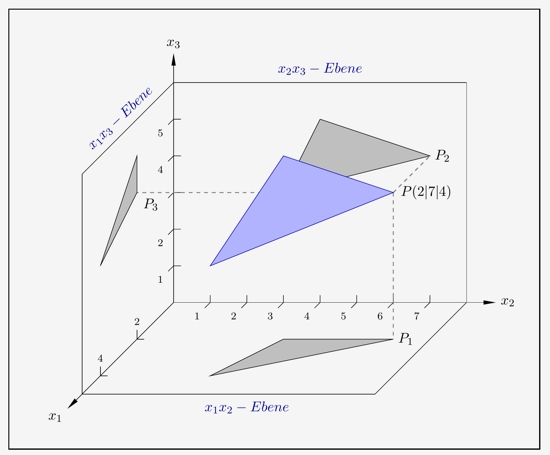
Betrachten wir zunächst die Projektion des Punktes \(P\) auf die \(x_1x_2\)-Ebene. Fällt Licht direkt von oben, so erscheint der Punkt \(P_1\) als Schattenpunkt auf der Koordinatenebene. Der \(x_1\)-Wert und der \(x_2\)-Wert bleiben erhalten, nur \(x_3\) wird zu Null. Entsprechend verhält es sich, wenn Licht direkt von vorne oder von rechts kommt.
Damit erhält der Punkt \(P(2|7|4)\)
- in der \(x_1x_2\)-Ebene den Schattenpunkt \(P_1(2|7|0)\)
- in der \(x_2x_3\)-Ebene den Schattenpunkt \(P_2(0|7|4)\)
- in der \(x_1x_3\)-Ebene den Schattenpunkt \(P_3(2|0|4)\)
Führt man das Ganze für alle 3 Punkte des Dreiecks durch, so erhält man die Schattenbilder auf den Koordinatenebenen.
\(\\[2em]\)
Projektion schräg auf eine Koordinatenebene
Parallel schräg einfallendes Sonnenlicht mit dem Vektor \(\overrightarrow{v}\) verläuft über die Spitze \(S\) einer Pyramide und projiziert den Schattenpunkt \(P\) auf die \(x_1x_2\)-Ebene. Die Kontur des Schattens entsteht durch die Verbindungen \(\overline{BP}\) und \(\overline{DP}\).
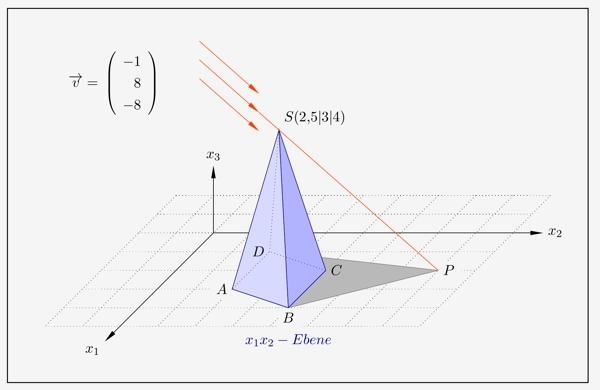
Zur Berechnung des Projektionspunktes \(P\) wird zunächst die Gerade \(g\) des Sonnenstrahls über die Spitze der Pyramide aufgestellt.
\( \quad \begin{array}{ l r c l } g: & \overrightarrow{x} & = & \overrightarrow{s} + t \cdot \overrightarrow{v} \\[4pt] & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 2{,}5 \\ 3 \\ 4 \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} -1 \\ 8 \\ -8 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Damit gilt
\( \quad \begin{array}{ r c c c r } x_1 & = & 2{,}5 & - & t \\[4pt] x_2 & = & 3 & + & 8t \\[4pt] x_3 & = & 4 & - & 8t \\ \end{array} \)
\(\\\)
Für alle Punkte in der \(x_1x_2\)-Ebene gilt nun \(x_3=0\). Für die Berechnung von \(P\) folgt
\( \quad \begin{array}{ r c l l } 0 & = & 4 - 8t & | \, + 8t \\[4pt] 8t & = & 4 & | \, : 8 \\[4pt] t & = & 0{,}5 \\ \end{array} \)
\(\\\)
\(t\) eingesetzt in die Gerade \(g\) ergibt
\( \quad \begin{array}{ r c l c c } \overrightarrow{p} & = & \begin{smallmatrix} \left( \begin{array}{c} 2{,}5 \\ 3 \\ 4 \end{array} \right) \end{smallmatrix} + 0{,}5 \cdot \begin{smallmatrix} \left( \begin{array}{r} -1 \\ 8 \\ -8 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 7 \\ 0 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Wir erhalten den Schattenpunkt \(P(2|7|0)\).
\(\\[2em]\)
Projektion auf 2 Koordinatenebenen
Projektion eines Objektes mit senkrechten Kanten auf eine senkrechte Koordinatenebene
Fällt paralleles Sonnenlicht, in diesem Fall direkt von rechts, in einem Raum, so kann sich der Schatten eines Objektes auf 2 Koordinatenebenen abbilden. Als Beispiel ist hier eine rechteckige Platte genommen, die senkrecht auf dem ebenen Boden steht. Die Ecken der Platte haben die Koordinaten
\( \quad \begin{array}{ l } A(2|3|0) \, , \; B(4|5|0) \, , \; C(4|5|4) \; \text{und} \; D(2|3|4). \\ \end{array} \)
\(\\\)
Das Sonnenlicht fällt mit dem Vektor \(\overrightarrow{v}\) ein.
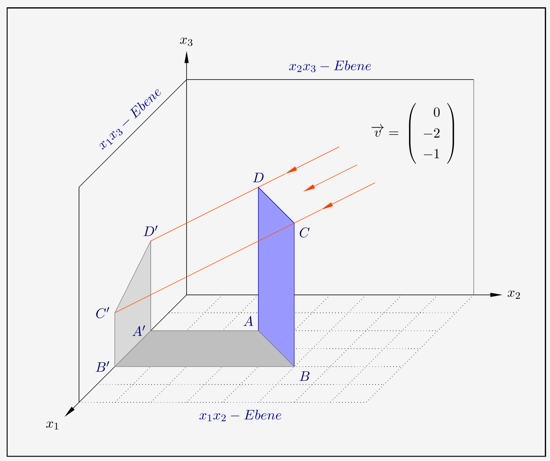
Um die Projektionspunkte \(C'\) und \(D'\) zu ermitteln, werden die Sonnenstrahlen über den Punkten \(C\) und \(D\) als Gerade aufgestellt.
\( \quad \begin{array}{ l r c l } g_{_C}: & \overrightarrow{x} & = & \overrightarrow{c} + r \cdot \overrightarrow{v} \\[10pt] & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 4 \\ 5 \\ 4 \end{array} \right) \end{smallmatrix} + r \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -2 \\ -1 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
\( \quad \begin{array}{ l r c l } g_{_D}: & \overrightarrow{x} & = & \overrightarrow{d} + s \cdot \overrightarrow{v} \\[8pt] & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -2 \\ -1 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Es gelten für \(g_{_C}\)
\( \quad \begin{array}{ r c l } x_1 & = & 4 \\[4pt] x_2 & = & 5 - 2r \\[4pt] x_3 & = & 4 - r \\ \end{array} \)
\(\\\)
und für \(g_{_D}\)
\( \quad \begin{array}{ r c l } x_1 & = & 2 \\[4pt] x_2 & = & 3 - 2s \\[4pt] x_3 & = & 4 - s \\ \end{array} \)
\(\\\)
Für alle Punkte in der \(x_1x_3\)-Ebene gilt \(x_2=0\). Für die Berechnung des Punktes \(C'\) folgt
\( \quad \begin{array}{ r c l l } 0 & = & 5 - 2r & | \, + 2r \\[4pt] 2r & = & 5 & | \, : 2 \\[4pt] r & = & 2{,}5 \\ \end{array} \)
\(\\\)
und für \(D'\) folgt
\( \quad \begin{array}{ r c l l } 0 & = & 3 - 2s & | \, + 2s \\[4pt] 2s & = & 3 & | \, : 2 \\[4pt] s & = & 1{,}5 \\ \end{array} \)
\(\\\)
\(r\) eingesetzt in die Gerade \(g_{_C}\) ergibt
\( \quad \begin{array}{ r c l c c } \overrightarrow{c'} & = & \begin{smallmatrix} \left( \begin{array}{c} 4 \\ 5 \\ 4 \end{array} \right) \end{smallmatrix} + 2{,}5 \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -2 \\ -1 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 4 \\ 0 \\ 1{,}5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
und \(s\) eingesetzt in die Gerade \(g_{_D}\) ergibt
\( \quad \begin{array}{ r c l c c } \overrightarrow{d'} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \right) \end{smallmatrix} + 1{,}5 \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -2 \\ -1 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 0 \\ 2{,}5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Wir erhalten die Punkte \(C'(4|0|1{,}5)\) und \(D'(2|0|2{,}5)\).
Da die Platte senkrecht auf der \(x_1x_2\)-Ebene steht und senkrechte Seiten hat und auch die \(x_1x_3\)-Ebene orthogonal zur \(x_1x_2\)-Ebene ist, können wir die Punkte \(A'\) und \(B'\) einfach ermitteln indem wir die Punkte \(C'\) und \(D'\) senkrecht nach unten auf die \(x_1\)-Achse projizieren. Es ergeben sich \(A'(2|0|0)\) und \(B'(4|0|0)\).
\(\\[1em]\)
Projektion eines Objektes mit schrägen Kanten auf eine senkrechte Koordinatenebene
Fällt paralleles Sonnenlicht, in diesem Fall schräg von vorne, in einem Raum, so kann sich der Schatten eines Objektes auf 2 Koordinatenebenen abbilden. In diesem Fall liegt abermals eine Pyramide vor.
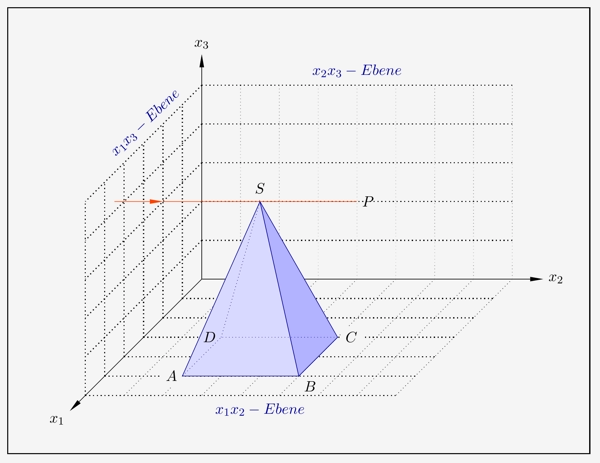
Wegen der 3D-Darstellung scheint das Licht von links zu kommen, was aber eine optische Täuschung ist. Um den Sachverhalt und die Konstruktion des Schattenverlaufs realistischer darstellen zu können, ist hier nun das Koordinatensystem gedreht. Es liegt eine Perspektive schräg von oben gesehen vor.
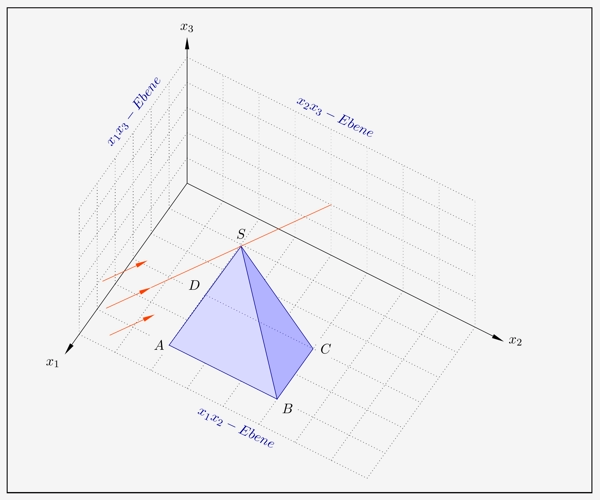
Die Eckpunkte der Pyramide lauten
\( \quad \begin{array}{ l } A(5|2|0) \, , \; B(5|5|0) \, , \; C(3|5|0) \, , \; D(3|2|0) \; \text{und} \; S(4|3{,}5|4). \\ \end{array} \)
\(\\\)
Das Sonnenlicht fällt mit dem Vektor \(\overrightarrow{v}= \begin{smallmatrix} \left( \begin{array}{r} -8 \\ 1 \\ -4 \end{array} \right) \end{smallmatrix} \) ein.
Der Schattenverlauf wird nun für jede Koordinatenebene gesondert ermittelt. Wir beginnen mit der \(x_1x_2\)-Ebene und blenden die senkrechten Koordinatenebenen zunächst einmal aus und berechnen den Projektionspunkt \(P\) des Sonnenstrahls über \(S\) auf die \(x_1x_2\)-Ebene.
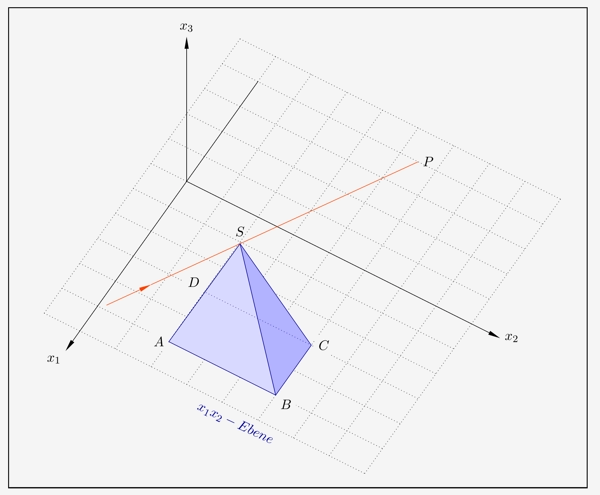
Wir stellen die Gerade \(g_{_S}\) über die Spitze \(S\) auf.
\( \quad \begin{array}{ l r c l } g_{_S}: & \overrightarrow{x} & = & \overrightarrow{s} + t \cdot \overrightarrow{v} \\[10pt] & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 4 \\ 3{,}5 \\ 4 \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} -8 \\ 1 \\ -4 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Es gilt nun \(x_3=0\) für
\( \quad \begin{array}{ r c l } x_3 & = & 4 - 4t \\ \end{array} \)
\(\\\)
Es folgt
\( \quad \begin{array}{ r c l l } 0 & = & 4 - 4t & | \, +4t \\[4pt] 4t & = & 4 & | \, :4 \\[4pt] t & = & 1 \\ \end{array} \)
\(\\\)
Eingesetzt in \(g_{_S}\) erhalten wir
\( \quad \begin{array}{ r c l c c } \overrightarrow{p} & = & \begin{smallmatrix} \left( \begin{array}{c} 4 \\ 3{,}5 \\ 4 \end{array} \right) \end{smallmatrix} + 1 \cdot \begin{smallmatrix} \left( \begin{array}{r} -8 \\ 1 \\ -4 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} -4 \\ 4{,}5 \\ 0 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Wir erhalten die Punkte \(P(-4|4{,}5|0)\).
Im Weiteren stellen wir die Gerade durch \(D\) und \(P\) sowie durch \(C\) und \(P\) auf. Da diese Geraden in der \(x_1x_2\)-Ebene verlaufen, ist stets \(x_3=0\). Das bedeutet, dass die dritte Koordinatenkomponente auch weggelassen werden kann (aber nicht muss).
\( \quad \begin{array}{ l r c l } g_{_{CP}}: & \overrightarrow{x} & = & \overrightarrow{c} + r \cdot \overrightarrow{CP} \\[10pt] & & = & \overrightarrow{c} +r \cdot \Big[\overrightarrow{p} - \overrightarrow{c}\Big] \\[10pt] & & = & \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 5 \end{array} \right) \end{smallmatrix} + r \cdot \left[ \begin{smallmatrix} \left( \begin{array}{c} -4 \\ 4{,}5 \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} 3 \\ 5 \end{array} \right) \end{smallmatrix} \right] \\[8pt] & & = & \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 5 \end{array} \right) \end{smallmatrix} + r \cdot \begin{smallmatrix} \left( \begin{array}{c} -7 \\ -0{,}5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
\( \quad \begin{array}{ l r c l } g_{_{DP}}: & \overrightarrow{x} & = & \overrightarrow{d} + s \cdot \overrightarrow{DP} \\[10pt] & & = & \overrightarrow{d} +s \cdot \Big[\overrightarrow{p} - \overrightarrow{d}\Big] \\[10pt] & & = & \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 2 \end{array} \right) \end{smallmatrix} + s \cdot \left[ \begin{smallmatrix} \left( \begin{array}{c} -4 \\ 4{,}5 \end{array} \right) \end{smallmatrix} - \begin{smallmatrix} \left( \begin{array}{r} 3 \\ 2 \end{array} \right) \end{smallmatrix} \right] \\[8pt] & & = & \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 2 \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{c} -7 \\ 2{,}5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
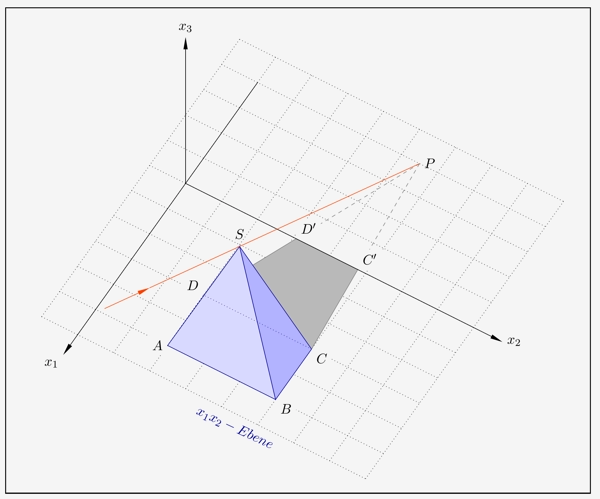
Der Schatten in der \(x_1x_2\)-Ebene verläuft zwischen den Geraden \(g_{_{CP}}\) und \(g_{_{DP}}\), allerdings nur bis zur \(x_2\)-Achse. Wir berechnen \(C'\) und \(D'\). Für beiden Punkte gilt \(x_1=0\).
Für \(C'\) ist
\( \quad \begin{array}{ r c l l } 0 & = & 3 - 7r & | \, +7t \\[4pt] 7r & = & 3 & | \, :7 \\[4pt] r & = & \frac{3}{7} \\ \end{array} \)
\(\\\)
eingesetzt in \(g_{_{CP}}\)
\( \quad \begin{array}{ l r c l c c } \overrightarrow{c'} & = & \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 5 \end{array} \right) \end{smallmatrix} + \frac{3}{7} \cdot \begin{smallmatrix} \left( \begin{array}{c} -7 \\ -0{,}5 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 0 \\ 4 \frac{11}{14} \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
und für \(D'\) ist
\( \quad \begin{array}{ r c l l } s & = & \frac{3}{7} \\ \end{array} \)
\(\\\)
eingesetzt in \(g_{_{DP}}\)
\( \quad \begin{array}{ l r c l c c } \overrightarrow{c'} & = & \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 2 \end{array} \right) \end{smallmatrix} + \frac{3}{7} \cdot \begin{smallmatrix} \left( \begin{array}{c} -7 \\ 2{,}5 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 0 \\ 3 \frac{1}{14} \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Damit liegen die Schattenpunkte auf der \(x_2\)-Achse \(C'\left(0\,\bigl|\,4 \frac{11}{14}\,\bigl|\,0\right)\) und \(D'\left(0\,\bigl|\,3 \frac{1}{14}\,\bigl|\,0\right)\) vor.
Abschließend fehlt noch die Spitze \(S\) projiziert mit dem Lichtstrahl auf die \(x_2x_3\)-Ebene mit dem Punkt \(P'\).
Wir nehmen wieder die Gerade \(g_{_S}\) mit
\( \quad \begin{array}{ r c l } \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 4 \\ 3{,}5 \\ 4 \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} -8 \\ 1 \\ -4 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
und setzen \(x_1=0\).
Es ergibt sich
\( \quad \begin{array}{ r c l l } 0 & = & 4 - 8t & | \, +8t \\[4pt] 8t & = & 4 & | \, :8 \\[4pt] t & = & 0{,}5 \\ \end{array} \)
\(\\\)
Eingesetzt in \(g_{_S}\) ist
\( \quad \begin{array}{ r c l c c } \overrightarrow{p'} & = & \begin{smallmatrix} \left( \begin{array}{c} 4 \\ 3{,}5 \\ 4 \end{array} \right) \end{smallmatrix} + 0{,}5 \cdot \begin{smallmatrix} \left( \begin{array}{r} -8 \\ 1 \\ -4 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 4 \\ 2 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
mit \(P'(0|4|2)\).
Es werden wieder alle Koordinatenebenen eingeblendet.
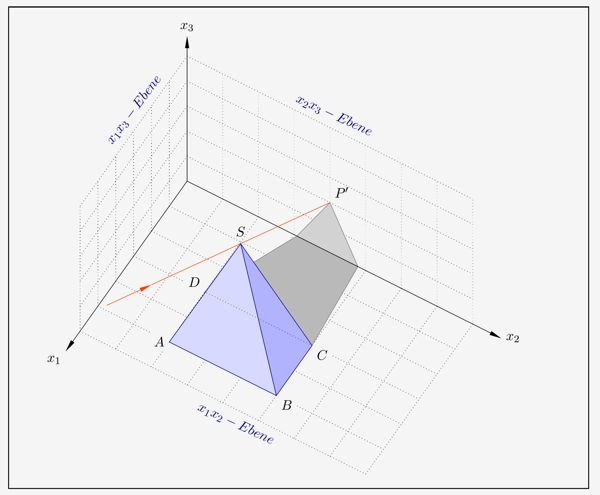
Zurück gedreht in die normale Ansicht ergibt sich
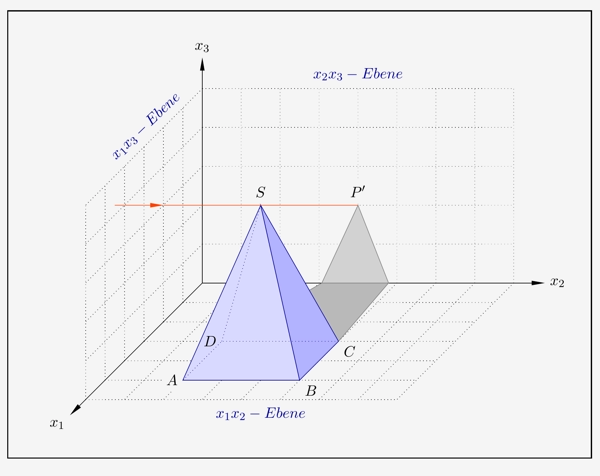
\(\\[2em]\)
Projektion auf eine allgemeine Ebene
Dies ist der einzige Fall, der nicht mit den Koordinatenebenen zusammenhängt. Da es hier aber ebenfalls darum geht, dass ein Lichtstrahl einen Schatten auf eine Ebene projiziert wird, rechne ich diesen auch den Projektionen zu. Es geht hier um ein schräges Dach mit einer senkrechten Antenne.
Das schräg von vorne einfallende Sonnenlicht mit dem Vektor \(\overrightarrow{v}\) projiziert einen Schatten der Antenne auf das Dach.
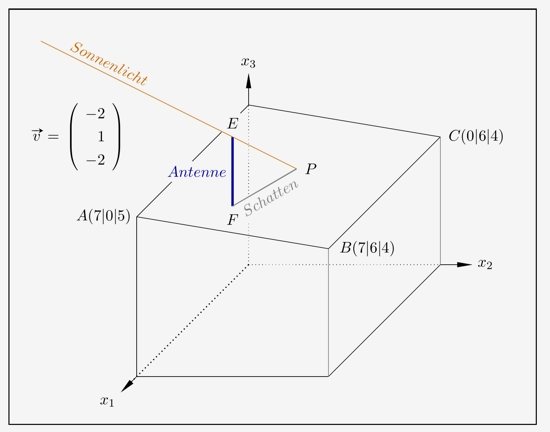
Die Antenne hat den Fußpunkt \(F(5|2|4{,}33)\) und den Endpunkt \(E(5|2|6{,}5)\).
Von der Berechnung des Punktes \(P\) her handelt es hier um den einfachen Schnittfall einer Geraden mit einer Ebene. Wir benötigen die Gerade mit
\( \quad \begin{array}{ l r c l } g: & \overrightarrow{x} & = & \overrightarrow{e} + t \cdot \overrightarrow{v} \\[10pt] & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 5 \\ 2 \\ 6{,}5 \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 1 \\ -2 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
und die Ebene der Dachfläche mit
\( \quad \begin{array}{ l r c l } D: & \overrightarrow{x} & = & \overrightarrow{b} + r \cdot \overrightarrow{BA} +s \cdot \overrightarrow{BC} \\[8pt] & \overrightarrow{x} & = & \overrightarrow{b} +r \cdot \Big( \overrightarrow{a} - \overrightarrow{b} \Big) +s \cdot \Big( \overrightarrow{c} - \overrightarrow{b} \Big) \\[8pt] & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 7 \\ 6 \\ 4 \end{array} \right) \end{smallmatrix} + r \cdot \left[ \begin{smallmatrix} \left( \begin{array}{r} 7 \\ 0 \\ 5 \end{array} \right) - \left( \begin{array}{r} 7 \\ 6 \\ 4 \end{array} \right) \end{smallmatrix} \right] + s \cdot \left[ \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 6 \\ 4 \end{array} \right) - \left( \begin{array}{r} 7 \\ 6 \\ 4 \end{array} \right) \end{smallmatrix} \right] \\[8pt] \quad ~ & \overrightarrow{x} & = & \begin{smallmatrix} \left( \begin{array}{c} 7 \\ 6 \\ 4 \end{array} \right) \end{smallmatrix} + r \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -6 \\ 1 \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{r} -7 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Zur Berechnung von \(P\) werden \(D\) und \(g\) gleichgesetzt
\( \quad \begin{array}{ c c l l } \begin{smallmatrix} \left( \begin{array}{c} 7 \\ 6 \\ 4 \end{array} \right) \end{smallmatrix} + r \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -6 \\ 1 \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{r} -7 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 5 \\ 2 \\ 6{,}5 \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 1 \\ -2 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
und vereinfacht.
\( \quad \begin{array}{ r c l l } \begin{smallmatrix} \left( \begin{array}{c} 7 \\ 6 \\ 4 \end{array} \right) \end{smallmatrix} + r \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -6 \\ 1 \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{r} -7 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 5 \\ 2 \\ 6{,}5 \end{array} \right) \end{smallmatrix} + t \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 1 \\ -2 \end{array} \right) \end{smallmatrix} & \Biggl| \; - t \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 1 \\ -2 \end{array} \right) \end{smallmatrix} \\[8pt] \begin{smallmatrix} \left( \begin{array}{c} 7 \\ 6 \\ 4 \end{array} \right) \end{smallmatrix} + r \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -6 \\ 1 \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{r} -7 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} - t \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 1 \\ -2 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 5 \\ 2 \\ 6{,}5 \end{array} \right) \end{smallmatrix} & \Biggl| \; - \begin{smallmatrix} \left( \begin{array}{r} 7 \\ 6 \\ 4 \end{array} \right) \end{smallmatrix} \\[8pt] r \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ -6 \\ 1 \end{array} \right) \end{smallmatrix} + s \cdot \begin{smallmatrix} \left( \begin{array}{r} -7 \\ 0 \\ 0 \end{array} \right) \end{smallmatrix} - t \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 1 \\ -2 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} -2 \\ -4 \\ 2{,}5 \end{array} \right) \end{smallmatrix} & \\ \end{array} \)
\(\\\)
Wir lösen das sich ergebende Gleichungssystem.
\( \qquad \begin{array}{ r ll c r c r c c c l } \textrm{I} \qquad ~ && & - & 7 \, s & + & 2 \, t & = & -2 \\[6pt] \end{array} \)
\( \quad \left. \begin{array}{ r r cc r c r c r c c } \textrm{II} && -6 \, r & & \qquad ~ & - & t & = & -4 \\[6pt] \textrm{III} && r & & \qquad ~ & + & 2 \, t & = & 2{,}5 && | \cdot 6 \\ \end{array} \quad \right]_{\Rightarrow \; \textrm{IV}}^+ \\ \)
\(\\\)
\( \quad \begin{array}{ r r cc r c r c c c c } \textrm{IV} \qquad ~ && \qquad ~ & & & & 11 \, t & = & 11 && | \, : 11 \\[6pt] && & & & & t & = & 1 \\ \end{array} \)
\(\\\)
\(t\) in \(\textrm{II}\) eingesetzt:
\( \quad \begin{array}{ r r r c r c r c r c l } \quad ~ && -6 \, r & & \qquad ~ & - & 1 & = & -4 && | \, +1 \\[6pt] && -6 \, r & & \qquad ~ & & & = & -3 && | \, : (-6) \\[6pt] && r & & \qquad ~ & & & = & 0{,}5 \\ \end{array} \)
\(\\\)
\(t\) in \(\textrm{I}\) eingesetzt:
\( \quad \begin{array}{ r r r c r c r c r c l } \qquad \quad ~ && & - & 7 \, s & + & 2 & = & -2 && | \, -2 \\[6pt] && & - & 7 \, s & & & = & -4 && | \, : (-7) \\[6pt] && & & s & & & = & \frac{4}{7} \\ \end{array} \)
\(\\\)
Es existiert genau ein Schnittpunkt zwischen der Gerade \(g\) und der Ebene \(D\). \(t\) in die Gerade eingesetzt ergibt
\( \quad \begin{array}{ l r c l c l } \overrightarrow{p} & = & \begin{smallmatrix} \left( \begin{array}{c} 5 \\ 2 \\ 6{,}5 \end{array} \right) \end{smallmatrix} + 1 \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 1 \\ -2 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 3 \\ 4{,}5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Der Projektionspunkt lautet \(P(3 | 3 | 4{,}5)\).
\(\\[1em]\)