Aufgabenstellung formulieren

\(\\\)

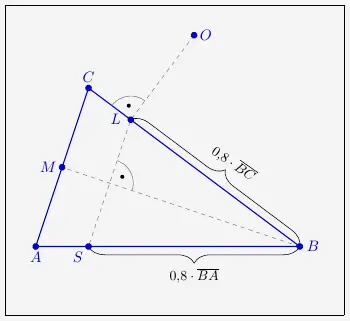
Betrachtet man die Grundfläche des Körpers mit der Grundfläche \(ABC\),

my image

\(\\\)

so ist die vordere Kante \(\overline{AB}\) (waagerecht gezeichnet) diejenige, an der der Körper später gedreht wird.

Mit der Gleichung

\( \quad \overrightarrow{BA} \circ \left[ \overrightarrow{OB} + r \cdot \overrightarrow{BA} - \overrightarrow{OC} \right] = 0 \quad \Longleftrightarrow \quad r = 0{,}8 \)

\(\\\)

wird hier der Lotfußpunkt \(L\) vom Koordinatenursprung auf die Strecke \(\overline{BC}\) berechnet mit dem Ergebnis \(r=0{,}8\).

Wie aus der Lösung der Aufgabe Dreieck ABC zu ersehen ist, sind das Dreiecke \(OCB\) und das gegenüber liegende Dreieck unter der Kante \(\overline{AB}\) kongruent und flächeninhaltsgleich. Das heißt, dass die Kanten \(\overline{CB}\) und \(\overline{AB}\) gleich lang sein müssen.

my image

Wird \(r=0{,}8\) in die Gleichung

\( \quad \overrightarrow{OS} = \overrightarrow{OB} + r \cdot \overrightarrow{BA} \)

\(\\\)

eingesetzt, so erhalten wir den Punkt \(S(4{,}8|3{,}6|0)\). Dieser ist zugleich der Spiegelpunkt von \(L\) mit der Spiegelachse der Strecke \(\overline{MB}\). \(M\) ist der Mittelpunkt der Strecke \(\overline{AC}\).

Wird der Körper nun wie beschrieben gedreht, also nach vorne um \(90^{\circ}\), so dass sich das Viereck \(ABED\) dann in der \(x_1x_2\)-Ebene befindet. Das Dreieck \(ABC\) steht dann aufrecht und orthogonal zu der \(x_1x_2\)-Ebene.

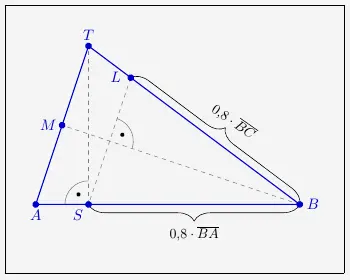
my image

Der Punkt \(T\) wird ermittelt mit

\( \quad \overrightarrow{OT} = \overrightarrow{OS} + \bigl|\overrightarrow{CS}\bigl| \cdot \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right) \end{smallmatrix} \)

\(\\\)

Das heißt, dass wir vom Punkt \(S\) senkrecht nach oben gehen mit der Strecke, die dem Abstand von \(S\) nach \(C\) entspricht. Dabei gelangen wir genau zu \(C\), der mit \(T\) identisch ist.

Wir können also auch sagen, dass \(S\) der Lotfußpunkt von \(C\) auf die Strecke \(\overline{AB}\) ist.

\(\\\)

Eine mögliche Aufgabenstellung wäre nun:

Berechne den Punkt \(T\), wobei folgende Voraussetzung erfüllt sein sollen:

\(\\[1em]\)