Reelle Zahl h
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Lage des Punktes
Der Punkt \(P_h\) liegt auf der \(x_3\)-Achse, wobei \(h\) die Höhe des Punktes angibt. Nach der Voraussetzung kann \(h\) dabei eine Höhe zwischen \(0\) und \(28\) haben.
\(\\[2em]\)
Aufgabe 2 – Werte von h

Liegt bei \(P_h\) ein rechter Winkel vor, so kann mit dem Satz des Pythagoras folgender Zusammenhang aufgestellt werden:
\( \quad \bigl|\overrightarrow{P_hB}\bigl|^2 + \bigl|\overrightarrow{P_hC}\bigl|^2 \; = \; \bigl|\overrightarrow{BC}\bigl|^2 \)
\(\\\)
Da \(B\) und \(C\) beide auf der gleichen Höhe liegen und der Quader symmetrisch um die \(x_3\)-Achse liegt (sowohl in \(x_1\)-Richtung als auch in \(x_2\)-Richtung), kann von
\( \quad \bigl|\overrightarrow{P_hB}\bigl| \; = \; \bigl|\overrightarrow{P_hC}\bigl| \)
\(\\\)
ausgegangen werden. Ferner wissen wir aus der Aufgabenlösung Ebene in Koordinatenform, dass Vektor
\( \quad \bigl|\overrightarrow{BC}\bigl| \; = \; \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} 22 \\ -22 \\ 0 \end{array} \right) \end{smallmatrix} \end{vmatrix} \)
\(\\\)
ist. Wir können die Gleichung vereinfachen und lösen in der folgenden Art:
\( \quad \begin{array}{ r c l l } \bigl|\overrightarrow{P_hB}\bigl|^2 + \bigl|\overrightarrow{P_hB}\bigl|^2 & = & \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} 22 \\ -22 \\ 0 \end{array} \right) \end{smallmatrix} \end{vmatrix}^2 \\[8pt] 2 \cdot \bigl|\overrightarrow{P_hB}\bigl|^2 & = & \left(\sqrt{22^2 + (-22)^2}\right)^2 \\[8pt] 2 \cdot \bigl|\overrightarrow{b} - \overrightarrow{p_h}\bigl|^2 & = & 22^2 + (-22)^2 \\[12pt] 2 \cdot \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} -11 \\ 11 \\ 28 \end{array} \right) \end{smallmatrix}- \begin{smallmatrix} \left( \begin{array}{r} 0 \\ 0 \\ h \end{array} \right) \end{smallmatrix} \end{vmatrix}^2 & = & 484 + 484 \\[12pt] 2 \cdot \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} -11 \\ 11 \\ 28 - h \end{array} \right) \end{smallmatrix} \end{vmatrix}^2 & = & 2 \cdot 484 & \Biggl| \, : 2 \\[10pt] \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{r} -11 \\ 11 \\ 28 - h \end{array} \right) \end{smallmatrix} \end{vmatrix}^2 & = & 484 \\[10pt] \left(\sqrt{(-11)^2 + 11^2 + (28 - h)^2}\right)^2 & = & 484 \\[10pt] (-11)^2 + 11^2 + (28 - h)^2 & = & 484 \\[8pt] 242 + (28 - h)^2 & = & 484 & \bigl| \, -242 \\[8pt] (28 - h)^2 & = & 242 & \bigl| \, \sqrt{\dots}\\[8pt] 28 - h & = & \pm \sqrt{242} & \bigl| \, -28 \\[8pt] -h & = & \pm \sqrt{242} -28 & \bigl| \, \cdot \, (-1) \\[8pt] h & = & 28 \pm \sqrt{242} \\[8pt] h_1 & \approx & 12{,}44 \\[8pt] h_2 & \approx & 43{,}56 \\[8pt] \end{array} \)
\(\\\)
Von den beiden Werten entspricht \(h_2\) nicht der Voraussetzung \(h<28\). Der einzig zulässige Wert ist also \(h = 28 - \sqrt{242} \approx 12{,}44\).
Ein stumpfer Winkel, dass heißt, ein Winkel zwischen 90° und 180°, entsteht für \(28 - \sqrt{242}<h<28\).
\(\\[2em]\)
Aufgabe 3 – Vorgehen zur Bestimmung von h
-
Die Gleichung
\( \quad \overrightarrow{OQ} \; = \; \begin{smallmatrix} \left( \begin{array}{r} 11 \\ 11 \\ 0 \end{array} \right) \end{smallmatrix} +t \cdot \begin{smallmatrix} \left( \begin{array}{r} -22 \\ 0 \\ 28 \end{array} \right) \end{smallmatrix} \; , \; t \in [0;1] \)
beschreibt einen Punkt \(Q\), der auf der Strecke \(\overline{AB}\) liegt. Denn es gilt
\( \quad \overrightarrow{a} \; = \; \begin{smallmatrix} \left( \begin{array}{r} 11 \\ 11 \\ 0 \end{array} \right) \end{smallmatrix} \)
und
\( \quad \begin{array}{ r c l c l c l } \overrightarrow{AB} & = & \overrightarrow{b} - \overrightarrow{a} & = & \begin{smallmatrix} \left( \begin{array}{r} -11 \\ 11 \\ 28 \end{array} \right) \end{smallmatrix}- \begin{smallmatrix} \left( \begin{array}{r} 11 \\ 11 \\ 0 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{r} -22 \\ 0 \\ 28 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
-
Weiter soll die Strecke \(\overline{P_hQ}\) orthogonal auf der Strecke \(\overline{AB}\) stehen und damit den kürztmöglichen Abstand gewährleisten.
\(\\\)
- Letzendlich ist die Strecke \(\overline{P_hQ}\) genauso lang wie die Strecke von \(P_h\) zum Mittelpunkt der Strecke \(\overline{BC}\).
\(\\\)
All diese Überlegungen sind in der nachfolgenden Skizze dargestellt.
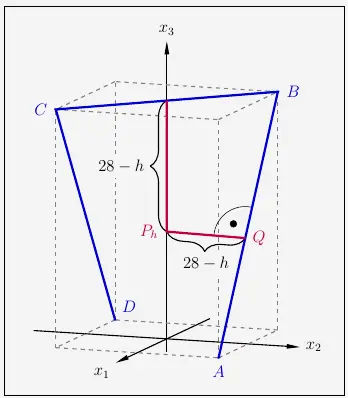
Aufgrund der Symmetrie bezüglich der \(x_3\)-Achse der Strecke \(\overline{AB}\) und der Strecke \(\overline{CD}\) würde der Abstand \(28-h\) auch für die Strecke \(\overline{CD}\) gelten. Das heißt, dass \(P_h\) zu allen 3 Strecken den gleichen Abstand hat.
Diese Überlegungen basieren auf den Grundgedanken des Lotfußpunktverfahrens: Bei dem Lotfußpunktverfahren wird der Punkt, in diesem Fall \(Q\), einer Geraden (Gerade durch \(A\) und \(B\)) gesucht, der orthogonal zu einem anderen Punkt, in diesem Fall \(P_h\), liegt. Der Punkt \(Q\) ist dann der von \(P_h\) auf die Gerade gelotete Punkt, der sogenannte Lotfußpunkt.
Für das Lotfußpunktverfahren müsste der Punkt \(P_h\) bekannt sein. Hier liegt der Fall nun anders. \(P_h\) ist nicht bekannt, dafür aber der Abstand von \(P_h\) nach \(Q\) in Abhängigkeit von \(h\). Damit lässt sich dann \(h\) berechnen, wenn auch sehr aufwändig.
\(\\\)