Tabelle der Binomialverteilung
Inhaltsverzeichnis
\(\\\)
Die Binomialverteilung liegt in den Tabellen als die Wahrscheinlichkeitsverteilung
\( \quad B_{n ; p}( k) \; = \, \begin{smallmatrix} \left( \begin{array}{c} n \\ k \end{array} \right) \end{smallmatrix} p^k \cdot (1-p)^{n-k} \) ,
\(\\\)
hier mit der Tabelle für \(n=10\), vor
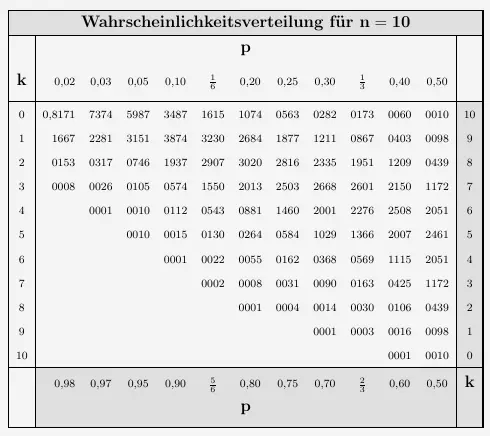
\(\\\)
oder liegt als kumulierte Tabelle,
\( \quad F_{n ; p}( k) \; = \, \displaystyle{\sum\limits_{i=0}^k} \begin{smallmatrix} \left( \begin{array}{c} n \\ i \end{array} \right) \end{smallmatrix} p^i \cdot (1-p)^{n-i} \) ,
\(\\\)
ebenfalls für \(n=10\), vor.
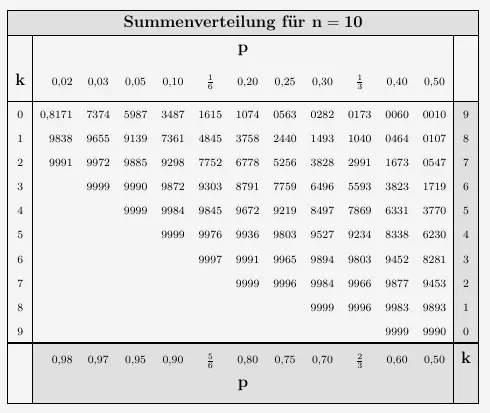
\(\\\)
Üblicherweise sind bei den Werten in der Tabelle nur die Nachkommastellen notiert, abgesehen von dem ersten Wert.
\(\\[2em]\)
Ablesen der Tabellenwerte
Die Tabellenwerte werden bei beiden Arten von Tabellen auf die gleiche Art abgelesen. Sei \(n=10\) und \(p=0{,}2\). Die Wahrscheinlichkeit für höchstens \(3\) Treffer mit
\( \quad P_{10 \, ; \, 0{,}2}( x \leq 3) \)
\(\\\)
wird folgendermaßen ermittelt. Es wird zunächst die Tabelle für \(n=10\) gewählt. In der Spalte \(k\) wird bei \(3\) nach rechts bis zur Spalte \(p=0{,}20\) gegangen.

\(\\\)
Es ergibt sich
\( \quad P_{10 \, ; \, 0{,}2}( x \leq 3) \, = \, 0{,}8791 \, = \, 87{,}91 \% \)
\(\\\)
Es ist zu erkennen, dass die \(p\)-Werte in der oberen Reihe nur bis \(p=0{,}5\) reichen. Für Werte mit einem größeren \(p\)-Wert wird die Wahrscheinlichkeit über die untere Reihe mit \(p\) ermittelt. Gleichzeitig wird dann die rechte Spalte für \(k\) genommen. Sei nun
\( \quad \begin{array}{ r c l } n & = & 10 \\ p & = & 0{,}7 \\ k & \leq & 4 \\ \end{array} \)
\(\\\)

\(\\\)
Wahrscheinlichkeiten, die von unten und rechts abgelesen werden (grau hinterlegt), müssen von \(1\) abgezogen werden. Damit gilt
\( \quad P_{10 \, ; \, 0{,}7}( x \leq 4) \, = \, 1 - 0{,}9527 \, = \, 0{,}0473 \, = \, 4{,}73 \% \)
\(\\[2em]\)
k mit der Tabelle ermitteln
Ist die Wahrscheinlichkeit vorgegeben und das \(k\) ist gesucht, geht man entsprechend umgekehrt vor. Sei nun
\( \quad \begin{array}{ r c l } n & = & 10 \\ p & = & \frac{1}{3} \\ \end{array} \)
\(\\\)
und
\( \quad P_{10 \, ; \, \frac{1}{3} }( x \leq k) \, \geq \, 0{,}9 \)
\(\\\)
Wir gehen dazu in die Spalte mit \(p = \frac{1}{3}\) und suchen die Wahrscheinlichkeit, bei der \(0{,}9\) zum ersten Mal erreicht bzw. überschritten wird. Gehen wir von dort aus zur Randspalte, so erhalten wir den \(k\)-Wert.

\(\\\)
Daraus folgt
\( \quad P_{10 \, ; \, \frac{1}{3} }( x \leq 5) \, \geq \, 0{,}9 \)
\(\\[1em]\)