Grenzwerte
Inhaltsverzeichnis
\(\\\)
Erläuterung des Grenzwertes
Um sich den Begriff des Grenzwertes zu erschließen, betrachten wir die Funktion \(f\) mit
\(\quad \begin{array}{ r c l } f(x) & = & \frac{1}{x} \\ \end{array} \)
für alle \(x \in \mathbb{R}\) mit \(x>0\).
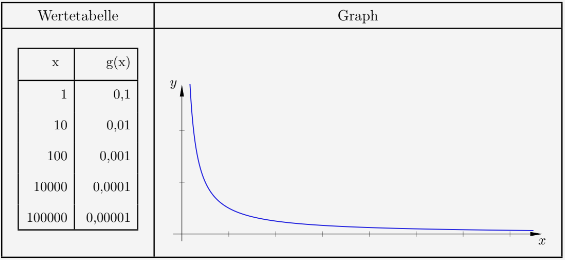
\(\\\)
Es ist zu erkennen, dass für größer werdende \(x\)-Werte der \(y\)-Wert immer kleiner wird. Strebt \(x\) gegen \(\infty\), so strebt \(f(x)\) gegen \(0\). Dieser Wert wird als der Grenzwert von \(f(x)\) genannt. Wir schreiben dies als
\(\quad \lim \limits_{x \to \infty} f(x) \; = \; 0 \)
\(\\\)
Beachte, das der Grenzwert kein Wert der Funktion sein muss. Denn \(f(x)\) erreicht ja nie die \(0\).
\(\\[1em]\)
Grenzwert bei Definitionslücken
Verschieben wir nun die Funktion \(f\) nach rechts und betrachten sie über den ganzen Bereich der reellen Zahlen.

\(\\\)
Diese neue Funktion sei \(g\) mit
\(\quad g(x) \; = \; \frac{1}{x-1} \)
\(\\\)
Es ist leicht zu erkennen, dass \(g\) an der Stelle \(x=1\) nicht definiert ist. Denn es gilt
\(\quad g(1) \; = \; \frac{1}{1-1} \; = \; \frac{1}{0} \)
\(\\\)
Das ist nicht definiert, da wir ja durch \(0\) nicht teilen können. Entsprechend haben wir in der Abbildung eine Definitionslücke bei \(x=1\). Es gilt für \(g\) der Definitionsbereich \(\mathbb{D} = \mathbb{R} \setminus \{1\}\).
\(\\[1em]\)
Rechtsseitiger und linksseitiger Grenzwert
Der Wert von \(g(1)\) kann nicht berechnet werden. Der Grenzwert für \(\lim \limits_{x \to 1}\) jedoch schon. Dabei betrachtet man den Grenzwert dafür, dass man von links gegen \(1\) geht und den Grenzwert dafür, dass man von rechts gegen \(1\) geht.
\(\\\)
Nähern wir uns der \(1\) von links, also mit \(x\)-Werten kleiner als \(1\), so schreiben wir \(\lim \limits_{x \uparrow 1}\) und bekommen
\(\quad \lim \limits_{x \uparrow 1} f(x) \; = \; -\infty \)
\(\\\)
Nähern wir uns der \(1\) dagegen von rechts, also mit \(x\)-Werten größer als \(1\), so schreiben wir \(\lim \limits_{x \downarrow 1}\) und bekommen
\(\quad \lim \limits_{x \downarrow 1} f(x) \; = \; \infty \)
\(\\\)
In der Literatur sind dafür auch andere Schreibweisen zu lesen, wobei ich diese gängige Schreibweise im Folgenden weiter verwenden werde.
\(\\\)
Ist
\(\quad \lim \limits_{x \uparrow x_0} f(x) \; = \; \lim \limits_{x \downarrow x_0} f(x)\, {,} \)
\(\\\)
so gilt
\(\quad \lim \limits_{x \to x_0} f(x) \)
\(\\\)
In diesem Fall trifft das für \(x_0=1\) nicht zu.
\(\\[1em]\)
Grenzwert für × strebt gegen Unendlich
Betrachten wir noch einmal, wie schon zu Beginn, \(\lim \limits_{x \to \infty}\). Im Bereich der reellen Zahlen sind \(-\infty\) und \(\infty\) ausgeschlossen. Denn nach der Definition vom Zahlenbereich \(\mathbb{R}\) gelten nur alle Zahlen zwischen \(-\infty\) und \(\infty\). Das heißt, dass wir für \(\pm \infty\) nur den Grenzwert bestimmen können.
\(\\\)
Da wir uns \(\infty\) nur von links und \(-\infty\) nur von rechts nähern können, schreiben wir vereinfacht, hier zum Beispiel bei der Funktion \(g\),
\(\quad \lim \limits_{x \to \infty} g(x) \; = \; 0 \)
\(\\\)
und
\(\quad \lim \limits_{x \to -\infty} g(x) \; = \; 0 \)
\(\\\)
Die Untersuchung der Grenzwerte \(\lim \limits_{x \to \pm \infty}\) nennt man auch die Randuntersuchung oder das Randverhalten einer Funktion.
\(\\[1em]\)